В.
Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Суперобложка /
Обложка /
Содержание

..Символы Веблена
Символы, которые мы
ввели в предыдущем разделе, называются символами Веблена.
Традиционно символы
Веблена вводятся формально, например так:
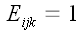 ,
для значений индексов i = 1, j = 2 и k = 3 и для
значений, которые получаются в результате их циклической
перестановки:
,
для значений индексов i = 1, j = 2 и k = 3 и для
значений, которые получаются в результате их циклической
перестановки: 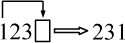 ,
, 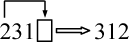 ;
;
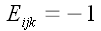 ,
для значений индексов i = 3, j = 2 и k = 1 и для
значений, которые получаются в результате их циклической
перестановки:
,
для значений индексов i = 3, j = 2 и k = 1 и для
значений, которые получаются в результате их циклической
перестановки: 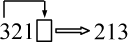 ,
, 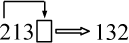 .
.
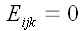 ,
если среди значений индексов имеются одинаковые числа.
,
если среди значений индексов имеются одинаковые числа.
В соответствии с нашим
определением, символ
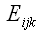 является определителем, составленным из столбцов единичной матрицы
является определителем, составленным из столбцов единичной матрицы
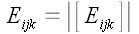 .
.
Определитель
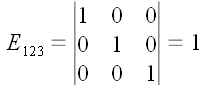 является определителем единичной матрицы с естественным порядком
столбцов. При перестановке двух его любых столбцов между собой он
изменит знак на противоположный. Если мы затем еще раз поменяем
местами два любые его столбца, то знак снова изменится.
Следовательно, определитель матрицы с четным количеством
перестановок столбцов будет равен единице, а с нечетным количеством
перестановок – минус единице. Выполняя последовательно
перестановки и не забывая каждый раз при этом изменять знак, мы
получим все ненулевые значения величин
является определителем единичной матрицы с естественным порядком
столбцов. При перестановке двух его любых столбцов между собой он
изменит знак на противоположный. Если мы затем еще раз поменяем
местами два любые его столбца, то знак снова изменится.
Следовательно, определитель матрицы с четным количеством
перестановок столбцов будет равен единице, а с нечетным количеством
перестановок – минус единице. Выполняя последовательно
перестановки и не забывая каждый раз при этом изменять знак, мы
получим все ненулевые значения величин
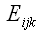 :
:
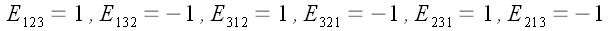 .
.
Естественно, что
символы с одинаковыми значениями индексов равны нулю, как
определители с одинаковыми столбцами.
Мы видим, что оба
определения приводят к одинаковому результату. Тем не менее,
неформальное определение, которого мы и дальше будем придерживаться,
позволяет использовать известные свойства определителей, что часто
бывает полезно.
..Свойства символов Веблена
Массив всех возможных
значений символов Веблена состоит из 27 элементов. К тому же
используется он при выполнении операций с другими массивами. Основная
проблема, которая возникает в таких случаях, – это непомерная
громоздкость реальных вычислений. Часто даже простые операции очень
трудно довести до конца без ошибок, возникающих при бесконечном
переписывании однообразных символов. Совершенно естественным при
таких обстоятельствах является стремление иметь больше разнообразных
возможностей для выполнения преобразований в самом общем виде и
краткой форме.
Возвращаясь к символам
Веблена, заметим, что у нас до сих пор нет удобного выражения для
определителя, составленного из произвольных столбцов единичной
матрицы. Мы без труда можем записать любой конкретный символ Веблена
с заданными числовыми значениями индексов, например:
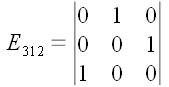 ,
но как записать определитель, соответствующий символу
,
но как записать определитель, соответствующий символу
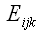 ?
?
И в этом вопросе
поможет уже известный нам символ Кронекера.
Символ Кронекера
используется в векторной алгебре в качестве индексного аналога
единичной матрицы.
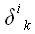 равен элементу единичной матрицы, стоящему на пересечении i-ой
строки и k-ого столбца. Поэтому единичную матрицу можно
записать с помощью символов Кронекера следующим образом:
равен элементу единичной матрицы, стоящему на пересечении i-ой
строки и k-ого столбца. Поэтому единичную матрицу можно
записать с помощью символов Кронекера следующим образом:
 .
.
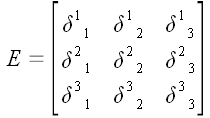
Следовательно, матрицу
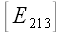 и матрицу
и матрицу
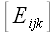 общего вида мы можем записать следующим образом:
общего вида мы можем записать следующим образом:
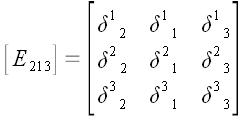 ,
,
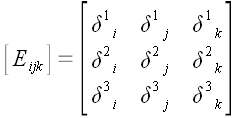 .
.
Аналогичным образом
может быть выражен и определитель
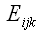 :
:
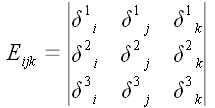 .
.
Подставляя конкретные
значения символов Кронекера, мы можем вычислить значения символов
Веблена. Тут важно только то, что мы это сделать можем, и результат
будет правильным, но конечно, мы этого делать не собираемся,
поскольку значения символов Веблена мы и без того знаем. А вот при
выполнении общих преобразований с произвольными символами такая
возможность нам не помешает. Посмотрим на конкретных примерах, как
это может нам помочь.
1. Умножение
произвольной матрицы на матрицу
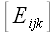 .
.
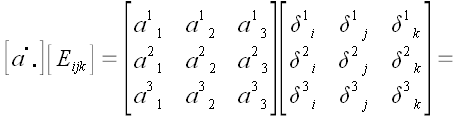
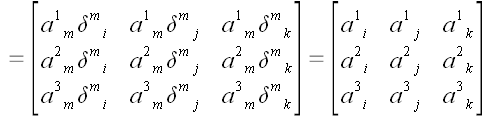 .
.
Мы воспользовались тем,
что
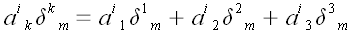 .
Из трех слагаемых не будет равен нулю только один, а именно тот, для
которого k = m.
Следовательно,
.
Из трех слагаемых не будет равен нулю только один, а именно тот, для
которого k = m.
Следовательно,
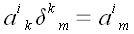 .
Формально свертывание любого вектора с символом Кронекера приводит к
замене индекса:
.
Формально свертывание любого вектора с символом Кронекера приводит к
замене индекса:
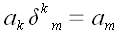 ,
,
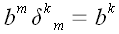 .
.
Правило
простое, но требует внимательности.
Необходимо
запомнить, что
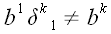 – в этом случае нельзя поставить знак равенства. Здесь
нет суммирования, это не свертка, это простое умножение одной из
координат вектора на символ
– в этом случае нельзя поставить знак равенства. Здесь
нет суммирования, это не свертка, это простое умножение одной из
координат вектора на символ
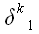 .
Произведению
.
Произведению
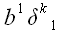 соответствуют целых три числа:
соответствуют целых три числа:
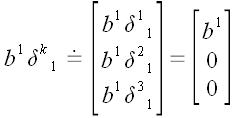 .
.
Возвращаясь к умножению матриц, отметим, что умножение произвольной
матрицы
 на матрицу
на матрицу
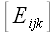 справа приводит к подстановке в ней столбцов. Первый ее столбец
заменяется на ее же i-ый столбец, второй столбец заменяется на
j-ый и третий, соответственно на k-ый.
справа приводит к подстановке в ней столбцов. Первый ее столбец
заменяется на ее же i-ый столбец, второй столбец заменяется на
j-ый и третий, соответственно на k-ый.
Для того, чтобы
отобразить это правило наглядно, введем следующее обозначение:
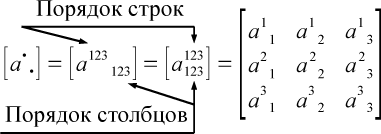 – матрица с естественным порядком строк и столбцов.
– матрица с естественным порядком строк и столбцов.
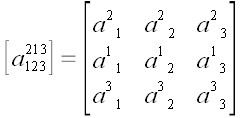 – в матрице переставлены первые две строки.
– в матрице переставлены первые две строки.
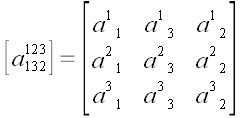 – переставлены вторые два столбца.
– переставлены вторые два столбца.
И наконец,
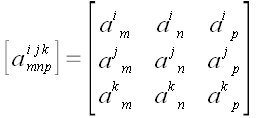 – матрица с произвольным образом переставленными строками и
столбцами.
– матрица с произвольным образом переставленными строками и
столбцами.
С учетом принятых
обозначений запишем:
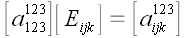 .
.
Аналогично можно
показать, что
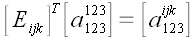 .
.
2. Докажем формулу
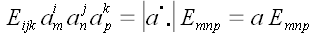 ,
где для краткости определитель с естественным порядком строк и
столбцов обозначен просто
,
где для краткости определитель с естественным порядком строк и
столбцов обозначен просто
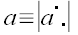 .
.
Прежде всего заметим,
что смысл выражения весьма прозрачен несмотря на кажущуюся сложность.
Мы знаем, что
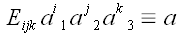 .
Соответственно
.
Соответственно
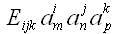 есть определитель, в котором первый столбец заменен столбцом m,
второй – столбцом n, а третий – k. Если
среди чисел m, n и p есть одинаковые, то
определитель и
есть определитель, в котором первый столбец заменен столбцом m,
второй – столбцом n, а третий – k. Если
среди чисел m, n и p есть одинаковые, то
определитель и
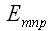 равны нулю. Если же среди этих чисел нет одинаковых, то определитель
равны нулю. Если же среди этих чисел нет одинаковых, то определитель
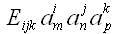 по модулю равен
по модулю равен
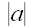 :
:
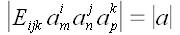 .
Это утверждение вытекает из того, что при перестановке столбцов
изменяется только знак определителя.
.
Это утверждение вытекает из того, что при перестановке столбцов
изменяется только знак определителя.
Чтобы доказать, что
формула справедлива всегда в том числе и с учетом знака, начнем с
очевидного тождества
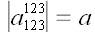 .
Умножим правую часть равенства на определитель единичной матрицы
.
Умножим правую часть равенства на определитель единичной матрицы
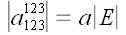 .
.
Теперь выполним одну и
ту же подстановку столбцов в обоих определителях:
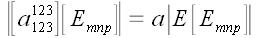 ,
но
,
но
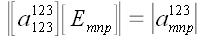 ,
а
,
а
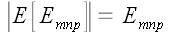 .
.
Откуда сразу следует,
что
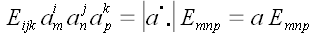 .
.
3. Докажем теорему об
определителях.
Определитель произведения двух квадратных матриц равен произведению
их определителей.
Это свойство
определителей доказывается в линейной алгебре, систематического
изложения которой мы не даем. Более того, данной теоремой мы уже не
один раз пользовались. Единственная цель, с которой мы приводим этот
вывод – продемонстрировать эффективность данного
математического языка при решении некоторых задач.
Пусть
 и
и
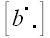 – две произвольные квадратные матрицы одинакового порядка, и
пусть
– две произвольные квадратные матрицы одинакового порядка, и
пусть
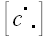 – матрица их произведения
– матрица их произведения
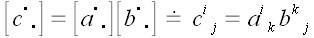 .
.
Тогда
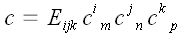 .
Развернем это равенство:
.
Развернем это равенство:
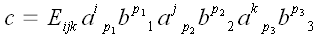 .
.
Теперь воспользуемся
тем, что
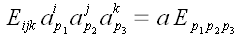 .
.
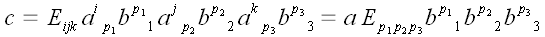 ,
но
,
но
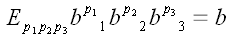 .
.
И мы получаем уже
известный результат: c = ab.
Желающие могут сравнить
данное доказательство с доказательством, которое можно найти в любом
учебнике по линейной алгебре, например, [19, с. 88].
4. Умножение двух
символов Веблена.
Умножим
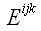 на
на
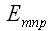 .
До сих пор индексы в символах Веблена мы всегда писали снизу. Для
векторов положение индексов имеет глубокий смысл, но для символов
Веблена, впрочем так же как и для символов Кронекера, положение
индексов не имеет никакого значения. Мы их пишем либо снизу, либо
сверху руководствуясь только соображениями удобства.
.
До сих пор индексы в символах Веблена мы всегда писали снизу. Для
векторов положение индексов имеет глубокий смысл, но для символов
Веблена, впрочем так же как и для символов Кронекера, положение
индексов не имеет никакого значения. Мы их пишем либо снизу, либо
сверху руководствуясь только соображениями удобства.
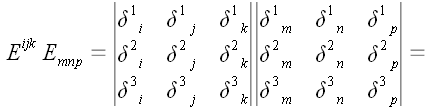
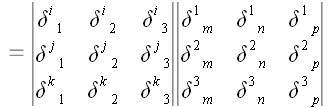 .
.
Здесь мы
воспользовались тем, что
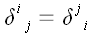 и
и
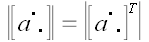 .
.
Теперь воспользуемся
теоремой об определителе произведения матриц.
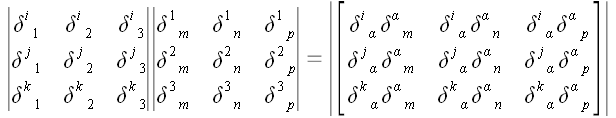 ;
;
Использовав свойства
символов Кронекера, упростим последний определитель:
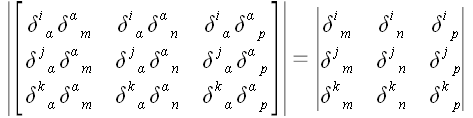 .
.
Полученное выражение
определяет возможные значения элементов шестимерного массива 36
чисел, и все это удовольствие – в одном выражении. Для записи
произведения
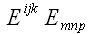 вводится специальный символ
вводится специальный символ
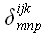 ,
который называется обобщенным символом Кронекера. В обобщенных
символах Кронекера нельзя поднимать и опускать индексы, поэтому не
имеет значения порядок верхних индексов по отношению к нижним и
наоборот. Обобщенные символы Кронекера определяются разными
способами, и не будет ошибки, если мы определим их так:
,
который называется обобщенным символом Кронекера. В обобщенных
символах Кронекера нельзя поднимать и опускать индексы, поэтому не
имеет значения порядок верхних индексов по отношению к нижним и
наоборот. Обобщенные символы Кронекера определяются разными
способами, и не будет ошибки, если мы определим их так:
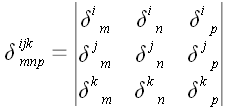 .
.
Использование
обобщенных символов Кронекера позволяет записать результат умножения
символов Веблена в более компактной форме:
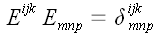 .
Обобщенный символ Кронекера может иметь меньшее количество верхних
или нижних индексов, чем размер определителя (при одинаковом
количестве верхних и нижних). В этом случае его следует понимать, как
определитель, составленный из элементов единичной матрицы, стоящих на
пересечении строк с номерами, совпадающими с верхними индексами, и
столбцов с номерами, совпадающими со значениями нижних индексов.
Например, на рис. 46* показано как
получается обобщенный символ Кронекера
.
Обобщенный символ Кронекера может иметь меньшее количество верхних
или нижних индексов, чем размер определителя (при одинаковом
количестве верхних и нижних). В этом случае его следует понимать, как
определитель, составленный из элементов единичной матрицы, стоящих на
пересечении строк с номерами, совпадающими с верхними индексами, и
столбцов с номерами, совпадающими со значениями нижних индексов.
Например, на рис. 46* показано как
получается обобщенный символ Кронекера
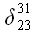 .
.
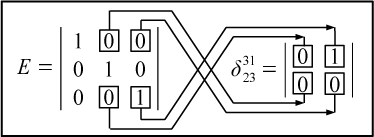 Рис. 46*
Рис. 46*
Матрицу,
соответствующую обобщенному символу Кронекера, т.е. единичную матрицу
с переставленными строками и столбцами, будем обозначать
соответственно:
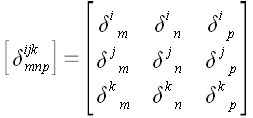 ,
следовательно,
,
следовательно,
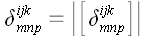
Свойства обобщенного
символа Кронекера легко выводятся из его определения, и мы на них не
будем останавливаться.
5. Свертка символов
Веблена по одному индексу.
Свернем символы Веблена
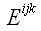 и
и
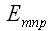 по последним индексам k и p.
по последним индексам k и p.
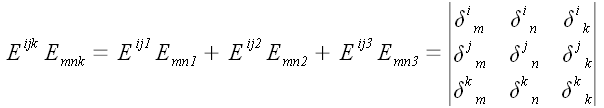
Разложим определитель
по последнему столбцу
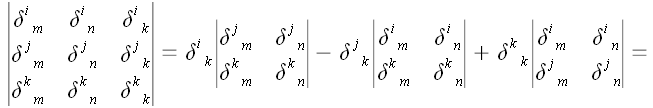
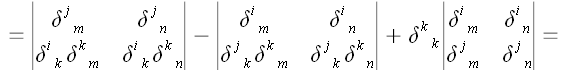
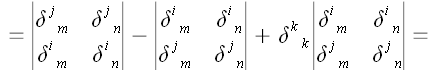
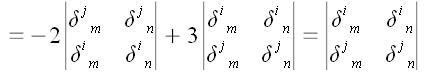
Мы воспользовались тем,
что
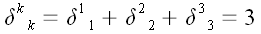 .
.
Следовательно, нам
удалось доказать, что
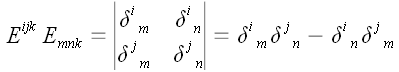 или, что то же самое,
или, что то же самое,
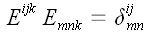 .
.
6. Свертка символов
Веблена по двум индексам.
Для того, чтобы найти
свертку по двум индексам
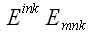 ,
воспользуемся предыдущим результатом:
,
воспользуемся предыдущим результатом:
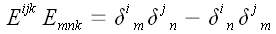 .
Полученный результат продолжаем сворачивать дальше, но теперь по
индексам j и n.
.
Полученный результат продолжаем сворачивать дальше, но теперь по
индексам j и n.
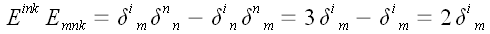 ,
следовательно,
,
следовательно,
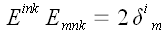 .
.
7. Свертка символов
Веблена по всем индексам.
Воспользуемся тем же
самым методом и свернем предыдущий результат еще раз
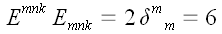 .
.
Пример.
Доказать равенство
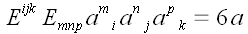 .
.
Так как
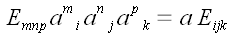 ,
то
,
то
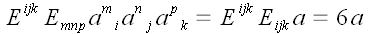 .
.
Прежде чем закончить
этот раздел, мы хотим вернуться к обобщенным символам Кронекера. Мы
почти ничего о них не говорили, и у нас до сих пор не нашлось для них
добрых слов. Чтобы хоть как-то загладить этот пробел, покажем, как с
их помощью можно получить общее выражение для алгебраических
дополнений.
Обозначим
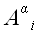 алгебраическое дополнение для элемента
алгебраическое дополнение для элемента
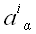 матрицы
матрицы
 .
.
Из курса линейной
алгебры нам известно, что
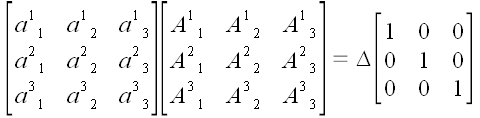 .
.
Запишем то же самое в
индексной форме:
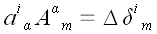 .
.
Далее воспользуемся
выражением
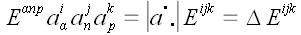 ,
в котором свернем правую и левую части с символом Веблена
,
в котором свернем правую и левую части с символом Веблена
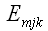 .
.
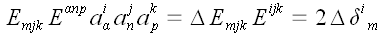
Преобразуем это
выражение.
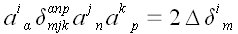
Теперь поделим правую и
левую части равенства на 2.
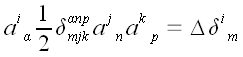 .
Сравнивая полученное выражение с
.
Сравнивая полученное выражение с
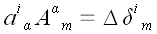 ,
делаем вывод, что
,
делаем вывод, что
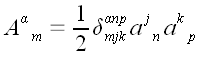 .
Произведя замену индексов для более удобного восприятия, окончательно
получаем, что алгебраическое дополнение
.
Произведя замену индексов для более удобного восприятия, окончательно
получаем, что алгебраическое дополнение
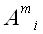 элемента
элемента
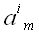 матрицы
матрицы
 равно
равно
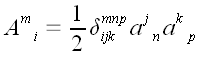 .
.
На этом знакомство с
символами Веблена закончим и перейдем к следующей важной теме.
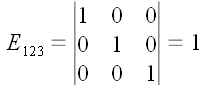 является определителем единичной матрицы с естественным порядком
столбцов. При перестановке двух его любых столбцов между собой он
изменит знак на противоположный. Если мы затем еще раз поменяем
местами два любые его столбца, то знак снова изменится.
Следовательно, определитель матрицы с четным количеством
перестановок столбцов будет равен единице, а с нечетным количеством
перестановок – минус единице. Выполняя последовательно
перестановки и не забывая каждый раз при этом изменять знак, мы
получим все ненулевые значения величин
является определителем единичной матрицы с естественным порядком
столбцов. При перестановке двух его любых столбцов между собой он
изменит знак на противоположный. Если мы затем еще раз поменяем
местами два любые его столбца, то знак снова изменится.
Следовательно, определитель матрицы с четным количеством
перестановок столбцов будет равен единице, а с нечетным количеством
перестановок – минус единице. Выполняя последовательно
перестановки и не забывая каждый раз при этом изменять знак, мы
получим все ненулевые значения величин
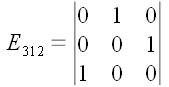 ,
но как записать определитель, соответствующий символу
,
но как записать определитель, соответствующий символу
 .
.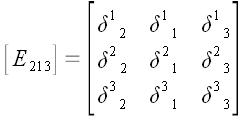 ,
,
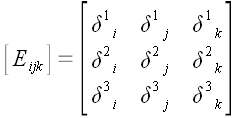 .
.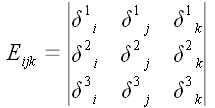 .
.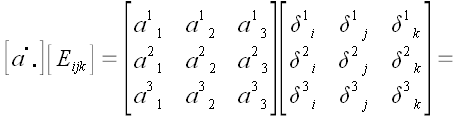
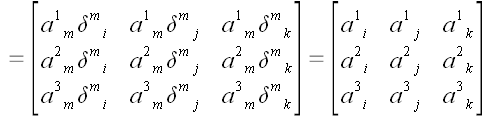 .
.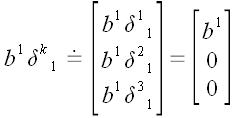 .
.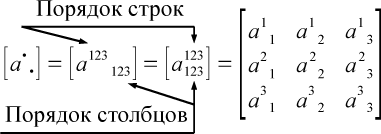 – матрица с естественным порядком строк и столбцов.
– матрица с естественным порядком строк и столбцов.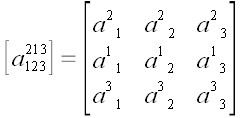 – в матрице переставлены первые две строки.
– в матрице переставлены первые две строки.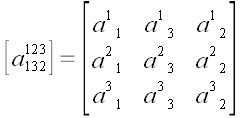 – переставлены вторые два столбца.
– переставлены вторые два столбца.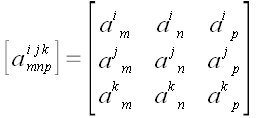 – матрица с произвольным образом переставленными строками и
столбцами.
– матрица с произвольным образом переставленными строками и
столбцами.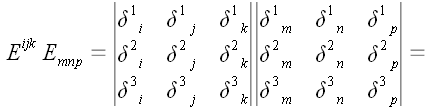
 .
.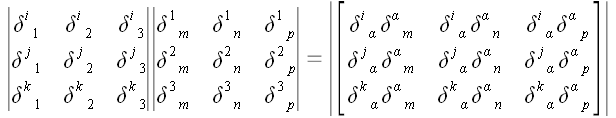 ;
; .
.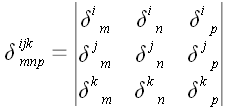 .
.
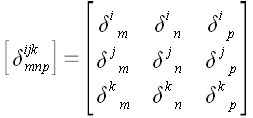 ,
следовательно,
,
следовательно,
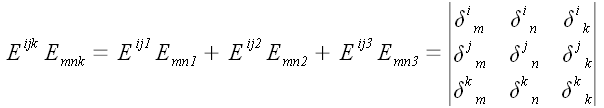
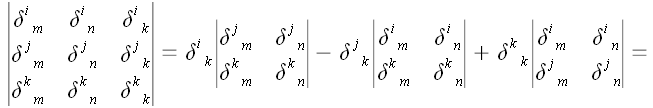
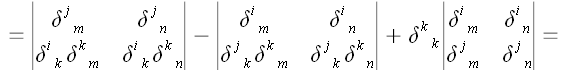
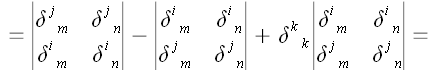
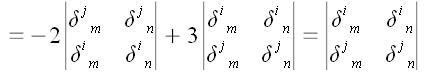
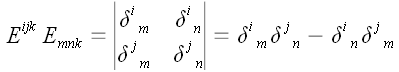 или, что то же самое,
или, что то же самое,
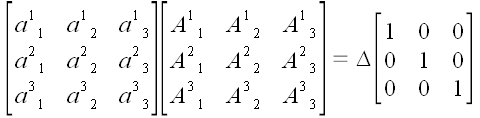 .
.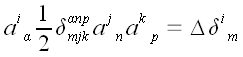 .
Сравнивая полученное выражение с
.
Сравнивая полученное выражение с
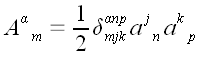 .
Произведя замену индексов для более удобного восприятия, окончательно
получаем, что алгебраическое дополнение
.
Произведя замену индексов для более удобного восприятия, окончательно
получаем, что алгебраическое дополнение
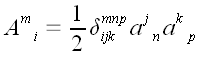 .
.