В.
Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Суперобложка /
Обложка /
Содержание

Эта
книга о тензорах, но не только о них. Еще никому не удавалось
написать книгу только о тензорах, потому что "тензор" –
это общее название для векторов, линейных операторов и даже для
скаляров. В книгах о тензорах, по необходимости, приходится говорить
об этом всем и еще, обычно, о матрицах, поскольку тензоры удобно
представлять в матричной форме. Поразмыслив над этой проблемой, мы
решили, что будем писать просто о векторах, как о самых понятных
тензорах, вводя постепенно и естественно, в связи с решаемыми
задачами, все необходимые атрибуты тензорной алгебры. И только в
конце книги мы приходим к общему определению тензора. И в тот момент,
когда мы это определение даем, оказывается, что все, что хотелось бы
сказать о тензорах в книге для начинающих, уже сказано раньше.
Тензоры широко применяются в
дифференциальной геометрии, теории относительности, механике,
электродинамике и других областях науки. В последнее время
предпринимаются попытки использовать теорию тензоров в экономических
науках. Интерес к теории тензоров возник в связи с работами
А. Эйнштейна по общей теории относительности и не угасает уже
почти сто лет. Конечно, за такое время было написано достаточно
хороших книг по этой теории. Есть книги для самых начинающих, и для
продвинутых, и для продолжающих, а глас вопиющего: "ну объясните
же в конце концов, что такое тензор, и как его можно представить",
– не умолкает.
Наша книга предназначена для
тех, кто еще не знает, что такое тензор, но по каким-то причинам
хочет это узнать. Мы стремились более объяснять, чем доказывать;
постепенно и не спеша, подходить к понятиям и их определениям, нежели
с них начинать. Следовательно, эта книга скорее для будущих инженеров
и физиков, нежели для математиков.
Объектом внимания физиков и
инженеров является природа, а не умозрительные построения, и,
поэтому, формализм и строгость в рассуждениях – непременные
атрибуты любой книги по математике – не являются для них
самоцелью. Они всего лишь средство, которое используется ровно в той
степени, в которой это бывает необходимо для правильного понимания
природы. Выразив свойства физических или технических объектов при
помощи математических понятий, физик и инженер наделяют эти понятия
более богатым содержанием, по сравнению с их математическими
определениями. В математике это недопустимо, в физике и технике иначе
просто не бывает.
Мы стремились сделать эту книгу
полезной прежде всего для будущих инженеров и физиков. Насколько нам
удалось, судить Вам, Читатель.
Физическая
наука изучает строение и свойства неживой природы. Объектами внимания
физических теорий являются физические системы, явления или процессы.
Количественные характеристики свойств физических объектов называются
физическими величинами. Физические величины обладают различным
уровнем сложности. Простые физические величины могут быть заданы
числовым значением и называются скалярными. Примерами скалярных
величин являются температура, масса, объем, площадь, длина, плотность
и т.д.
Сложные физические величины не могут быть заданы одним числовым
значением. Например, для того, чтобы определить такие величины как
сила, скорость, ускорение нам необходимо задать по три числовых
значения для каждой величины. Эти величины и аналогичные им мы
называем векторными.
Векторные величины весьма разнообразны. Кроме силы, скорости и
ускорения, о которых мы уже упомянули, к векторным величинам
относятся перемещение, импульс силы, импульс тела, угловая скорость и
ускорение, момент силы и момент импульса и многие другие.
Сконцентрировав внимание на наиболее общих свойствах, присущих всем
без исключения векторным величинам безотносительно к их физической и
геометрической природе, мы приходим к понятию вектора. Теория
векторов, как отвлеченных идеальных объектов, является разделом
математики.
Скалярные и векторные величины не исчерпывают всего многообразия
величин, которые необходимы современной науке. В чем-то родственными
векторам, но в общем случае более сложными являются тензорные
величины. Примерами тензорных величин являются напряженное состояние
в точке, упругость твердого тела, момент инерции, диэлектрическая
проницаемость... Для определения таких величин необходимо задать
целую таблицу числовых значений. Абстрагируясь от конкретного
физического и геометрического содержания таких величин, мы приходим к
понятию тензора. Тензор, как и вектор, является математическим
понятием и предметом изучения тензорной и векторной алгебры. Понятие
тензора настолько крепко связано с идеями векторной алгебры, что,
допустив однажды в теорию векторные величины, мы были обречены, в
конце концов, прийти к тензорам. Открыв для себя тензоры, мы
обнаружили, что все физические величины, так или иначе, являются
тензорными, даже самые привычные из них. А мы, постоянно пользуясь
ими, даже и не догадывались об этом. Это открытие можно сравнить
разве что с открытием господина Журдена из знаменитой комедии
Мольера, который был потрясен, когда узнал, что более сорока лет
говорит прозой, не подозревая об этом.
Векторная и тензорная алгебры очень тесно связаны. Тензорная алгебра,
являясь непосредственным развитием и обобщением векторной, включает
ее в себя как важный частный случай. Векторная алгебра, став частью
тензорной, серьезно изменила свой облик за счет появления новых
выразительных средств. К тому же в ней пришлось изменить некоторые
акценты. Поэтому изучение тензорной алгебры логично и удобно начинать
с самого начала – с векторов. К тензорам мы придем постепенно,
сделав при этом экскурсы в теорию матриц и рассмотрев некоторые
содержательные примеры.
.Геометрическое определение вектора
Вектор
традиционно определяется как направленный отрезок [1, 9,
12,14]. Например,
А.Н. Рублев дает такое определение:
"Вектор представляет собой геометрический объект,
характеризуемый длиной и направлением" [14,
с. 88].
Это определение фокусирует внимание на двух, несомненно важных
свойствах всех физических векторных величин, – они все
характеризуются некоторым количественным значением, которое
отождествляется с длиной отрезка, и направлением в пространстве. При
своих несомненных достоинствах – простота и наглядность –
это определение не отражает в полной мере существа понятия "вектор".
Во-первых, у физических и геометрических объектов можно обнаружить
немало свойств, которые характеризуются величиной и направлением, но,
тем не менее, не являющихся векторными. Например, положение
транспортных средств на карте города можно показать при помощи
направленных отрезков, связав их длину с длиной транспортного
средства. Такие направленные отрезки будут в целом правильно отражать
движение транспортных потоков, но для них нельзя разумным образом
ввести традиционные для векторной алгебры алгебраические операции.
Еще один пример. Для того, чтобы однозначно задать величину и
направление поворота твердого тела, можно воспользоваться
направленным отрезком. Для этого достаточно длину отрезка
отождествить с величиной угла поворота и направить его вдоль оси
поворота в сторону, откуда вращение видно против часовой стрелки.
Если мы совершаем последовательно несколько поворотов тела
относительно различных осей, то каждый такой поворот может быть задан
соответствующим направленным отрезком. Если эти направленные отрезки
сложить по правилам векторной алгебры, то мы снова получим
направленный отрезок. К сожалению, его нельзя интерпретировать как
результат последовательных поворотов тела. Операция сложения таких
геометрических отрезков не имеет геометрического смысла.
Точно так же как "короля делает свита", алгебраические
операции превращают направленный отрезок в вектор. До тех пор, пока
мы такие операции не ввели и не изучили их свойства, мы не можем,
строго говоря, утверждать, что направленный отрезок является
вектором.
Во-вторых, нельзя утверждать также, что вектор является
геометрическим объектом. Направленный отрезок, несомненно, является
геометрическим объектом, хотя и малоинтересным. Над геометрическими
объектами нельзя выполнять алгебраические действия. Нельзя, скажем,
сложить трапецию с пирамидой или умножить шар на квадрат. Вводя
алгебраические операции над направленными отрезками, мы определяем
новый математический объект, который не является больше объектом
геометрическим. Направленный отрезок превращается при этом в условное
изображение этого нового объекта. Между тем, нельзя недооценивать
практическое значение этого образа. Он придает конкретный
геометрический смысл алгебраическим преобразованиям. Видимо,
правильнее считать, что вектор имеет двойственную природу – он
одновременно является и алгебраическим и геометрическим объектом.
Если мы согласны с предыдущими рассуждениями, то мы должны и
согласиться с тем, что определение вектора задача непростая, и к ней
лучше подойти постепенно и осторожно, начиная издалека, хотя бы с
уточнения понятия направленного отрезка.
Определение (1)
Под направленным отрезком будем понимать определенным образом
ориентированный в пространстве отрезок, один из концов которого
называется началом, а второй его концом.
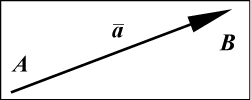 Рис. 1
Рис. 1
Обозначение:
направленный отрезок будем обозначать буквой любого алфавита с
чертой, например,
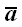 .
Если A начальная точка
отрезка, а B конечная, то
направленный отрезок можно обозначить как
.
Если A начальная точка
отрезка, а B конечная, то
направленный отрезок можно обозначить как
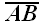 .
.
Определение (2)
Длина направленного отрезка называется его модулем.
Обозначение:
модуль вектора
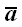 обозначается
обозначается
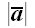 или просто a , а модуль вектора
или просто a , а модуль вектора
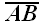 обозначается
обозначается
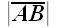 .
.
Определение (3)
Два направленных отрезка будем считать равными, если они могут быть
совмещены при помощи параллельного переноса и при этом начало одного
совпадает с началом другого.
Определение (4)
Если отрезки могут быть совмещены при помощи параллельного переноса,
но при этом начало одного совмещается с концом другого, то такие
отрезки будем называть противоположными.
Другими словами, одинаковые направленные отрезки имеют одинаковые
модули или длины, параллельны между собой и одинаково направлены. При
этом они могут занимать различные положения в пространстве.
Определение (5)
Направленный отрезок, начало и конец которого совпадают, называется
нулевым направленным отрезком.
Нулевой направленный отрезок может быть назван отрезком лишь с
большой натяжкой. Раз его начало и конец совпадают, то это скорее
точка, а не отрезок. Да и направления никакого он не имеет. Однако,
для полноты картины он весьма полезен, в чем мы убедимся в
дальнейшем. Обозначается нулевой отрезок нулем с чертой –
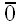 .
Модуль нулевого отрезка естественно равен нулю –
.
Модуль нулевого отрезка естественно равен нулю –
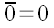 .
.
.Алгебраические
операции над направленными
отрезками
До
сих пор мы стремились найти однозначное отображение в научном языке
очевидных фактов из жизни направленных отрезков. Любая научная теория
начинается с этого. Любая теория начинается с научных фактов, которые
должны быть ясно и однозначно сформулированы. Направленный отрезок –
это относительно простой объект, и все что о нем можно было сказать,
мы уже сказали. Теперь нам предстоит решить важную задачу –
превратить хоть и направленный, но все еще простой, отрезок в вектор.
Для этого необходимо ввести над направленными отрезками
алгебраические операции.
Правила действий, которые мы собираемся ввести, не являются ни
очевидными, ни произвольными. Свое обоснование они имеют в реальных
свойствах физических величин, таких как сила, скорость и ускорение.
..Сложение направленных отрезков
Определение (6)
Направленные отрезки складываются по правилу параллелограмма или, что
одно и то же, по правилу треугольника. Несколько направленных
отрезков можно складывать по правилу многоугольника (рис. 2).
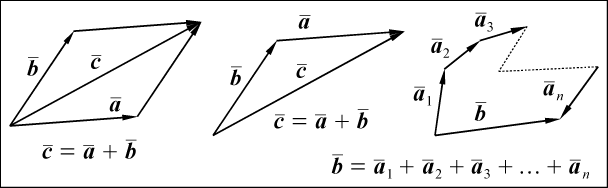 Рис. 2
Рис. 2
Свойства операции сложения
1. Перестановочность (коммутативность)
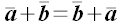
2. Сочетательность (ассоциативность)
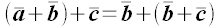
Свойства непосредственно следуют из определения.
..Умножение направленных отрезков на число
Определение (7)
Произведением направленного отрезка
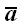 на число
на число
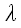 является отрезок
является отрезок
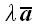 ,
модуль которого равен произведению модуля
,
модуль которого равен произведению модуля
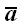 на модуль
на модуль
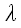 ,
а направление совпадает с направлением отрезка
,
а направление совпадает с направлением отрезка
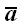 ,
если
,
если
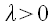 ,
и противоположно
,
и противоположно
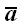 ,
если
,
если
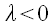 .
При
.
При
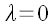 или
или
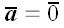 считаем, что
считаем, что
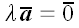 .
.
Из определения сразу вытекает, что
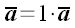 .
.
Обратный или противоположный отрезок мы определили как отрезок равный
по модулю, но противоположный данному. Если
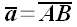 ,
то отрезок противоположный ему будет
,
то отрезок противоположный ему будет
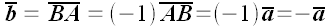 .
То есть отрезок противоположный отрезку
.
То есть отрезок противоположный отрезку
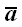 есть отрезок
есть отрезок
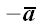 .
А по определению нулевого отрезка мы получаем
.
А по определению нулевого отрезка мы получаем
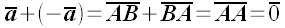 (рис.3).
(рис.3).
 Рис. 3
Рис. 3
Между прочим, вполне обычные алгебраические свойства. Но в том то вся
и прелесть, что для таких необычных объектов, как направленные
отрезки, мы получили привычные и давно известные из повседневного
опыта обращения с обычными числами алгебраические свойства. Следующие
свойства также являются вполне очевидными.
Свойства операции умножения
1. Сочетательность (ассоциативность)
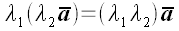
2. Распределительность (дистрибутивность) относительно чисел
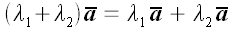
3. Распределительность (дистрибутивность) относительно направленных
отрезков
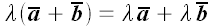
Разобравшись с действиями, которые можно выполнять с направленными
отрезками, мы готовы дать определение геометрического вектора.
Определение геометрического вектора (8)
Направленные отрезки, для которых определены операции сложения и
умножения на число в соответствии с определениями 6
и 7, называются геометрическими векторами.
Наверное, стул, кресло, табуретку, пуфик и скамейку можно назвать
одним общим словом седалище. (Вообще-то, в современном языке смысл
этого слова другой, а в древности так называли место для сидения.)
Если мы так поступим, то на вопрос – как представить седалище?
На что оно похоже? – мы сможем только пожать плечами. Каждый
раз, переходя к более общим понятиям, мы теряем в образности
представлений. Мы только что определили геометрический вектор. Физика
дает нам другие многочисленные примеры векторов: вектор скорости,
ускорения, силы, напряженности поля и т.д. Выделив в этих понятиях
наиболее важное и общее и отвлекаясь от частного конкретного
содержания, мы приходим к общему определению вектора. Но что есть
общего между всеми этими примерами конкретных векторов? Все эти
векторы имеют размер, направление и для них определены операции
сложения и умножения на число. Оказывается, однако, что свойства
связанные с размерами векторов, и свойства, вытекающие из их
алгебраической природы, являются независимыми. Поэтому, все, что
связано с размерами, математики предпочитают изучать отдельно, в так
называемых метрических теориях. Алгебраические же свойства векторов
становятся при этом предметом изучения теории линейных или векторных
пространств. В результате, мы приходим к следующему определению
вектора.
Общее определение вектора (9)
|
Объекты любой
природы, для которых определены операции сложения и умножения на
число, и, которые в свою очередь обладают следующими свойствами:
|
|
1.
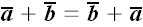 ; ;
2.
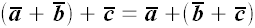 ; ;
3.
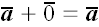 ; ;
4.
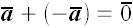 ; ;
|
5.
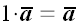 ; ;
6.
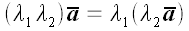 ; ;
7.
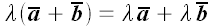 ; ;
8.
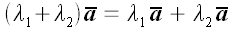 , ,
|
|
называются векторами.
|
В свете данного определения, векторами могут считаться многочлены
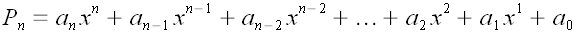 ,
вектор-строки
,
вектор-строки
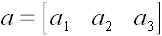 и вектор-столбцы
и вектор-столбцы
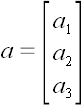 .
.
Такая "всеядность" нового определения не может не сказаться
на пищеварении и, при неумелом обращении, может грозить расстройством
желудка. В дальнейшем мы будем оставаться в рамках геометрической
теории векторов, однако, связь между векторами и матрицами, которую
устанавливает общее определение, мы не будем упускать из вида.




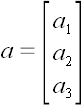 .
.