В.
Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Суперобложка /
Обложка /
Содержание

.Проекции вектора
Слово
"проекция" происходит от латинского "projectio"
– бросание вперед. Идея этого понятия возникла, видимо, при
наблюдении теней, которые отбрасывают освещенные предметы (рис. 4).
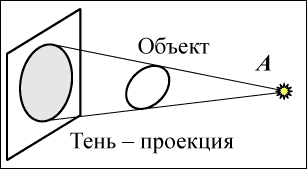 Рис. 4
Рис. 4
Способ проекции, изображенный на рис. 4 называется центральной
проекцией. Если источник света А отнести достаточно
далеко, то мы получим параллельную проекцию. Параллельная проекция
обладает рядом полезных качеств, в силу чего находит широкое
применение в инженерной практике. Мы тоже в дальнейшем будем говорить
только о параллельной проекции, опуская ее полное название.
..Параллельное проектирование вектора в плоскости
Рассмотрим для начала наиболее простой, но тем не менее важный
для понимания, частный случай – проектирование объектов целиком
расположенных в плоскости на прямую, также расположенную в этой же
плоскости. Направление проектирования зададим при помощи вектора
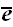 .
.
На рис. 5 показаны проекции точки A,
отрезка BC и вектора
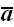 на прямую L.
на прямую L.
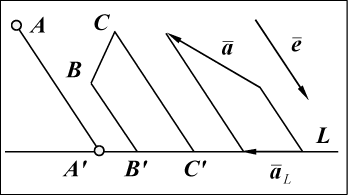 Рис. 5
Рис. 5
Из рисунка видно, что проекцией точки A
на прямую L является точка
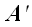 ,
проекцией отрезка BC является
отрезок
,
проекцией отрезка BC является
отрезок
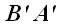 ,
а проекцией вектора
,
а проекцией вектора
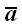 является вектор
является вектор
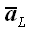 .
.
Параллельную проекцию вектора
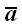 на прямую L по направлению
на прямую L по направлению
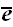 будем обозначать
будем обозначать
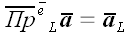 .
.
Теперь дадим необходимые определения.
Определение проекции точки (10)
Пусть точка A,
прямая L, и
вектор
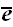 лежат в одной плоскости. Проекцией точки A
на прямую L в направлении
вектора
лежат в одной плоскости. Проекцией точки A
на прямую L в направлении
вектора
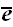 в этом случае будем называть точку
в этом случае будем называть точку
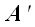 ,
которая является результатом пересечения прямой L
и прямой, проведенной через точку A
в направлении вектора
,
которая является результатом пересечения прямой L
и прямой, проведенной через точку A
в направлении вектора
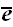 .
.
Определение проекции вектора на прямую (11)
Пусть вектор
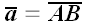 ,
прямая L, и
вектор
,
прямая L, и
вектор
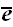 лежат в одной плоскости. Проекцией вектора
лежат в одной плоскости. Проекцией вектора
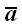 на прямую L в направлении
вектора
на прямую L в направлении
вектора
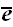 в этом случае будем называть вектор
в этом случае будем называть вектор
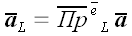 ,
равный вектору
,
равный вектору
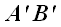 .
Точки
.
Точки
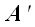 и
и
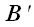 при этом являются проекциями начала и конца вектора
при этом являются проекциями начала и конца вектора
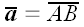 на прямую L.
на прямую L.
Для векторов, лежащих на одной прямой, возможны лишь два направления:
либо в одну, либо в другую сторону – третьего не дано. В этом
случае само понятие вектора становится излишним, и можно вполне
обойтись лишь алгебраическим значением – числом со знаком.
Правда, для этого на прямой необходимо сначала задать одно из
направлений в качестве положительного.
Определение направленной оси (12)
Прямая, с заданным на ней положительным направлением, называется
направленной осью или просто осью.
Определение алгебраического значения проекции вектора на
направленную ось (13)
Алгебраическим значением проекции вектора на направленную ось
называется модуль проекции вектора на эту ось, взятый со знаком "+",
если направление проекции вектора совпадает с положительным
направлением оси, и со знаком "–", в противном
случае.
Обозначать алгебраическое значение проекции вектора на ось будем
точно так же, как проекцию вектора на прямую, только без "векторной"
черты сверху, например:
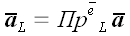 .
.
Проекция вектора на ось – это вектор. Алгебраическое значение
проекции вектора на ось – это число. Последнее название
является исключительно громоздким, но пользуясь тем, что из контекста
обычно всегда ясно, о чем идет речь – о числе или о векторе –
и то и другое будем, в тех случаях, когда это не вызывает
недоразумений, называть просто проекцией вектора.
Теорема о проекции суммы векторов на ось
Проекция суммы векторов на ось равна сумме их проекций.
В данном случае из контекста теоремы неясно, о какого типа проекциях
идет речь. Но к счастью, данная теорема справедлива и для векторной
проекции и для алгебраической. А вот доказательства для этих случаев
будут различные. Для начала докажем теорему для векторных проекций.
Рассмотрим для определенности сумму четырех векторов (рис. 6).
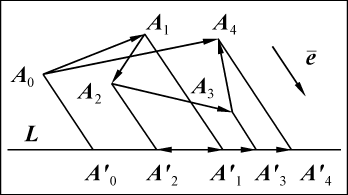 Рис. 6
Рис. 6
Из рис. 6 видно, что:
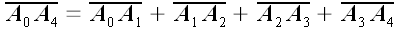 ,
,
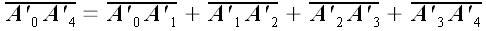 ,
,
в соответствии с правилами сложения векторов.
С другой стороны:
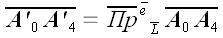 ;
;
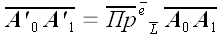 ;
;
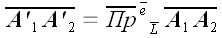 ;
;
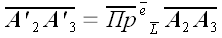 ;
;
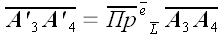 .
.
Следовательно,
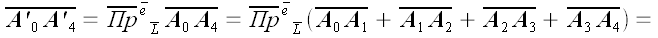
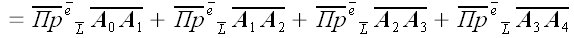 .
.
Тот же самый результат может быть получен для любого количества
векторов, что дает нам право записать теорему в общем виде:
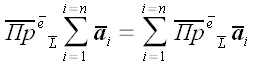 .
.
Теперь мы можем доказать теорему об алгебраических значениях
проекций. Пусть
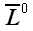 – единичный вектор, совпадающий с направлением оси
– единичный вектор, совпадающий с направлением оси
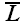 .
Такой вектор обычно называется ортом-вектором. Тогда векторную
проекцию произвольного вектора
.
Такой вектор обычно называется ортом-вектором. Тогда векторную
проекцию произвольного вектора
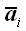 на ось
на ось
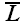 можно записать как:
можно записать как:
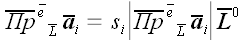 ,
где s означает знак.
,
где s означает знак.
Поскольку
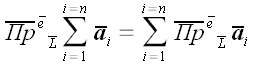 ,
то
,
то
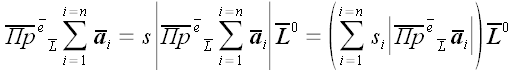 .
Но модуль проекции вектора на ось, взятый с соответствующим знаком, –
это и есть по определению алгебраическая величина проекции вектора на
ось. Следовательно,
.
Но модуль проекции вектора на ось, взятый с соответствующим знаком, –
это и есть по определению алгебраическая величина проекции вектора на
ось. Следовательно,
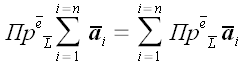 .
.
Запишем теперь обе формулировки доказанной нами теоремы в
символической форме:
|
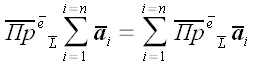 ; ;
|
(1)
|
|
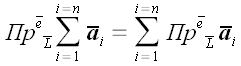 . .
|
(2)
|
Как видим, и в символической записи эти две теоремы очень похожи, но
разница, тем не менее, есть. В первом случае справа и слева от знака
равенства стоят векторы, а во втором – числа.
Вообще то, эта теорема относится к той категории теорем, в которых
то, что требуется доказать, гораздо более очевидно, чем само
доказательство. Так или иначе, теорема полезная, и в дальнейшем
она нам еще пригодится.




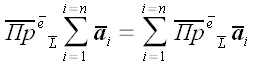 .
.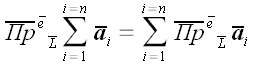 ,
то
,
то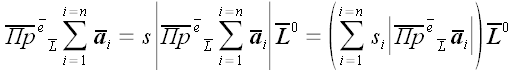 .
Но модуль проекции вектора на ось, взятый с соответствующим знаком, –
это и есть по определению алгебраическая величина проекции вектора на
ось. Следовательно,
.
Но модуль проекции вектора на ось, взятый с соответствующим знаком, –
это и есть по определению алгебраическая величина проекции вектора на
ось. Следовательно,
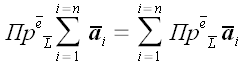 .
.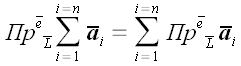 .
.