В.
Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Суперобложка /
Обложка /
Содержание
|
|
|

Теорию
векторов мы начали с геометрического определения вектора. После этого
мы ввели понятие координат вектора. При этом мы убедились, что
координатная форма часто оказывается чрезвычайно удобной для
конкретных вычислений с векторами. Нами получены правила для
скалярного и векторного умножения векторов в координатной форме.
Найдены формулы, выражающие площадь параллелограмма и объем
параллелепипеда через координаты векторов. Координатная форма
является настолько удобной, что даже само определение вектора часто
дается через его координатное представление. В этом случае вектор
определяется как некий физический или геометрический объект, который
может быть задан при помощи своих координат, связанных с определенной
координатной системой. Между тем до настоящего момента только
линейные операции с векторами мы могли выполнять в произвольных
координатах. Все остальные правила, позволяющие выполнять действия с
векторами в координатной форме, получены только для специальных
ортонормированных координатных систем. В дальнейшем мы избавимся от
этого ограничения, но прежде нам придется изучить законы
преобразования координат векторов при смене координатных систем.
Допустим, что у нас имеется две координатные системы. Одну из этих
систем, неважно какую именно, будем называть первой или старой
координатной системой. Вторую, только для того, чтобы отличить от
первой, будем называть второй или новой. Векторы базиса первой
координатной системы будем обозначать
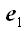 ,
,
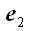 и
и
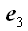 .
Соответственно, векторы второй системы будем обозначать
.
Соответственно, векторы второй системы будем обозначать
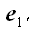 ,
,
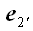 ,
,
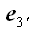 – со штрихами над индексами. Базисные векторы первой системы мы
можем выразить через векторы базиса второй, и наоборот.
– со штрихами над индексами. Базисные векторы первой системы мы
можем выразить через векторы базиса второй, и наоборот.
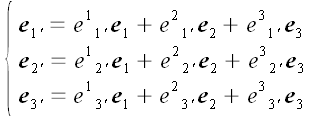 ;
;
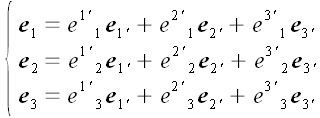 .
.
Символами
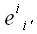 обозначены соответствующие координаты
обозначены соответствующие координаты
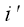 -
ого (нового) вектора в старой системе координат, а символами
-
ого (нового) вектора в старой системе координат, а символами
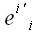 координаты
координаты
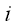 -
ого (старого) вектора в новой системе координат (рис. 39).
-
ого (старого) вектора в новой системе координат (рис. 39).
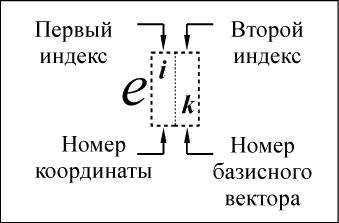 Рис. 39
Рис. 39
В соответствии с соглашением А. Эйнштейна о суммировании по
повторяющимся индексам данные системы можно записать короче:
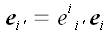 и
и
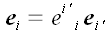 .
.
Имея две координатные системы, мы произвольный вектор
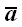 можем разложить по каждой из них:
можем разложить по каждой из них:
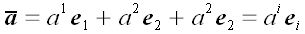 ;
;
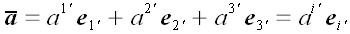 .
.
Выразим в первом равенстве векторы старого через векторы нового
базиса.
|
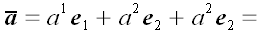
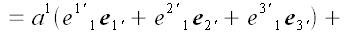
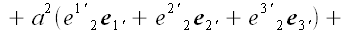
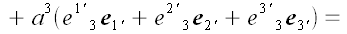
|
Приведем подобные
|
|
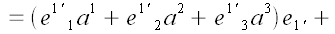
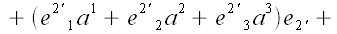
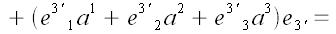
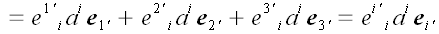
|
Используем соглашение о суммировании по повторяющимся индексам
|
Выражения в скобках, стоящие перед базисными векторами, представляют
собой координаты вектора
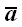 в новой системе координат, выраженные через координаты того же
вектора в старой системе координат.
в новой системе координат, выраженные через координаты того же
вектора в старой системе координат.
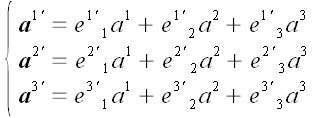
Совершенно аналогично получаются выражения координат вектора
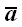 в старом базисе через его же координаты в новом.
в старом базисе через его же координаты в новом.
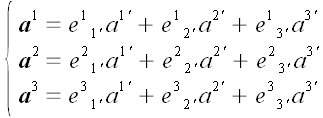
Полученные равенства удобнее записывать в матричной форме.
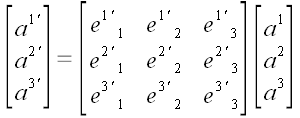 и
и
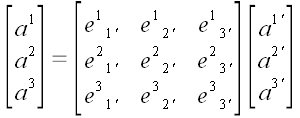 .
.
Формулы, связывающие значения координат вектора в различных
координатных системах, называют прямым и обратным преобразованием
координат вектора. При этом, не имеет значения, которое
преобразование является прямым, а которое обратным. Важно, что эти
преобразования являются взаимно обратными по отношению друг к другу.
Используя два последних матричных равенства, мы можем записать:
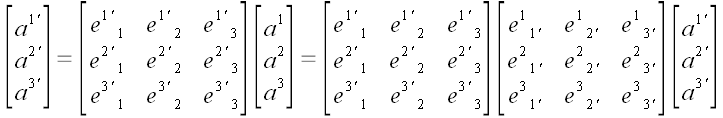 .
.
Откуда следует, что
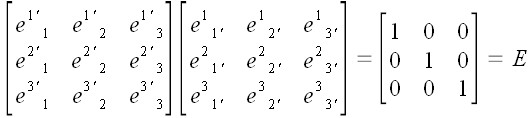 ,
где E, как
,
где E, как
обычно, означает единичную матрицу. То есть, прямому и обратному
преобразованию соответствуют взаимно обратные матрицы.
Несмотря на то, что матричная запись является намного компактнее
полностью развернутой, но и она во многих теоретических
преобразованиях излишне громоздка. Наиболее компактной является форма
записи с использованием соглашения о суммировании – в
дальнейшем мы ее будем называть индексной формой. Запишем последнее
равенство в индексной форме:
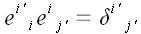 .
Значок, стоящий в правой части, называется "дельтой Кронекера".
.
Значок, стоящий в правой части, называется "дельтой Кронекера".
Дельта Кронекера определяется следующим образом:
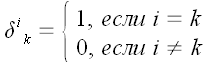 .
.
В дальнейшем мы часто будем показывать, как выглядят те или иные
выражения в различных формах записи, поскольку, хотя индексная форма
и короче, а векторная нагляднее, матричная удобнее, когда дело
доходит непосредственно до вычислений. Каждая из форм записи имеет
свои неоспоримые преимущества и, так или иначе, используется в
векторной алгебре.
Иногда одни и те же преобразования мы будем выполнять параллельно с
использованием различных форм записи. Мы надеемся, что это поможет
оценить достоинства каждой из них.
Итак, суммируем введенные нами обозначения и основные результаты.
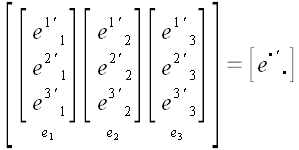
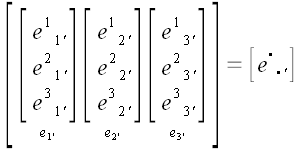
Матрица преобразования координат в подробной и символической записи.
 ;
;
 .
.
Каждый из столбцов составлен из координат соответствующих базисных
векторов одной из систем координат (новой или старой) в другой
системе координат.
Произвольный вектор в различных системах координат.
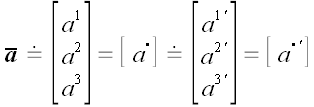 .
.
Матрицы прямого и обратного преобразования координат являются взаимно
обратными.
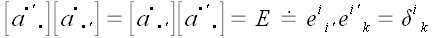 .
.
Формулы преобразования координат вектора при переходе от старой
системы координат к новой и обратно.
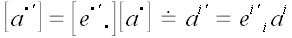 и
и
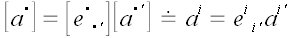
В некотором смысле матрицы
 и
и
 являются матрицами тождественного преобразования: они преобразуют
вектор, заданный своими координатами в одной координатной системе, в
тот же самый вектор, но через координаты в другой координатной
системе. Поэтому, неслучайно матрицы
являются матрицами тождественного преобразования: они преобразуют
вектор, заданный своими координатами в одной координатной системе, в
тот же самый вектор, но через координаты в другой координатной
системе. Поэтому, неслучайно матрицы
 ,
,
 и матрицу тождественного преобразования E
мы обозначаем одной и той же буквой латинского алфавита.
и матрицу тождественного преобразования E
мы обозначаем одной и той же буквой латинского алфавита.
Пример
на
определение
матрицы
преобразования
координат.
Пусть ∆ABC – произвольный
треугольник (рис. 40). Точка О – точка пересечения медиан
AD и CE. В
качестве первоначальной или "старой" системы координат
выберем векторы
 и
и
 ,
совпадающих со сторонами AB и AC
треугольника. Пусть векторы базиса новой системы координат
,
совпадающих со сторонами AB и AC
треугольника. Пусть векторы базиса новой системы координат
 и
и
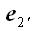 совпадают с отрезками медиан OB и OD
соответственно. Попробуем найти матрицу преобразования координат,
прямую и обратную.
совпадают с отрезками медиан OB и OD
соответственно. Попробуем найти матрицу преобразования координат,
прямую и обратную.
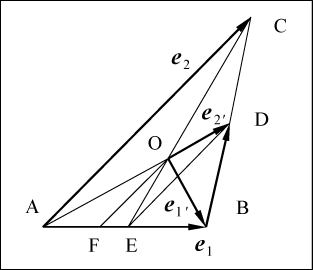 Рис. 40
Рис. 40
Для этого нам потребуется разложить векторы нового базиса по векторам
старого. Параллельная проекция вектора
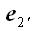 на вектор
на вектор
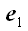 по направлению вектора
по направлению вектора
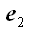 совпадает с отрезком FE. Так как по условию
CE медиана, то отрезок AE
равен половине
совпадает с отрезком FE. Так как по условию
CE медиана, то отрезок AE
равен половине
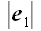 ,
а так как в точке пересечения медианы делятся в отношении 1:3, то
отрезок FE равен 1/3 от этой половины:
,
а так как в точке пересечения медианы делятся в отношении 1:3, то
отрезок FE равен 1/3 от этой половины:
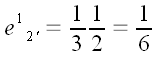 .
Аналогично
.
Аналогично
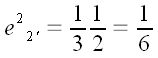 .
.
Параллельная проекция вектора
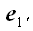 на вектор
на вектор
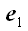 совпадает с отрезком FB, что составляет
совпадает с отрезком FB, что составляет
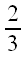 от длины вектора
от длины вектора
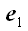 ,
поэтому,
,
поэтому,
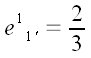 .
Проекция вектора
.
Проекция вектора
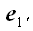 на вектор
на вектор
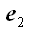 по направлению параллельному
по направлению параллельному
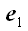 составляет
составляет
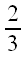 от половины длины вектора
от половины длины вектора
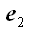 и противоположна к
и противоположна к
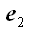 по направлению. Все это дает возможность записать для координат
векторов нового базиса следующие выражения:
по направлению. Все это дает возможность записать для координат
векторов нового базиса следующие выражения:
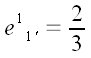 ;
;
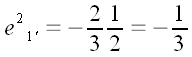 ;
;
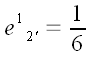 ;
;
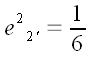 .
.
Полученные координаты позволяют выразить новые векторы через старые в
векторной
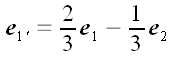 и
и
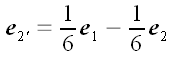 ;
;
и координатной
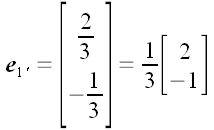 ;
;
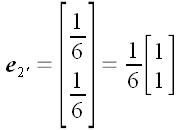
формах.
Теперь мы можем записать матрицу преобразования координат:
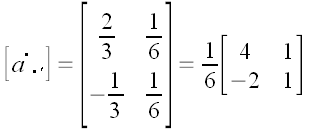 .
.
Полученную матрицу можно использовать для вычисления координат
векторов в старой системе координат по известным координатам в новой
системе. Например, вектор
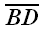 в новой системе имеет координаты:
в новой системе имеет координаты:
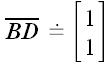 .
.
Следовательно, в старой мы получим:
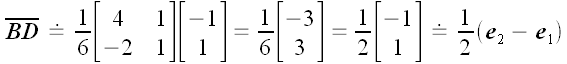 .
.
Для нахождения обратного преобразования нам необходимо найти обратную
матрицу.
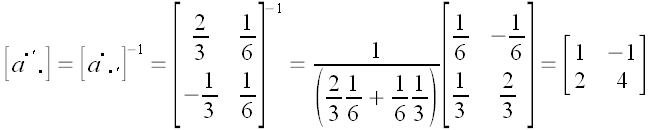 .
.
Опять же легко проверить, что, умножая на матрицу координат вектора
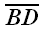 в старой системе, мы получим координаты того же вектора в новой
системе:
в старой системе, мы получим координаты того же вектора в новой
системе:
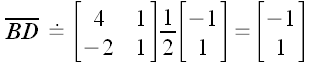 .
.
Пример
на
определение
матрицы
преобразования
координат
для
случая,
когда
одна
из
систем
координат
является
декартовой.
Этот случай является менее общим, но он обладает большим практическим
значением, так как на практике в качестве одной из координатных
систем мы чаще всего выбираем декартову систему координат.
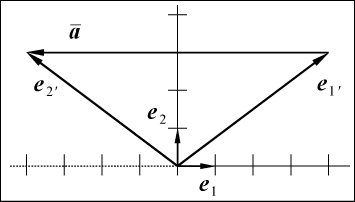 Рис. 41
Рис. 41
Пусть в качестве основной системы координат выбрана декартова система
с базисными векторами
 и
и
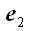 .
.
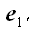 и
и
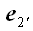 – базисные векторы новой системы координат, координаты которых
относительно старой системы координат нам известны (рис. 41):
– базисные векторы новой системы координат, координаты которых
относительно старой системы координат нам известны (рис. 41):
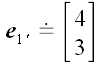 ,
,
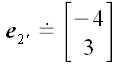 .
.
Из координат этих векторов легко составить матрицу преобразования
координат:
 .
.
Декартова система координат особенная и для того, чтобы подчеркнуть
это, мы в обозначении матрицы преобразования от произвольной системы
к декартовой будем точку заменять на звездочку:
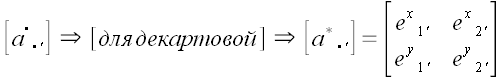 .
.
Соответственно, обратную к ней будем обозначать так:
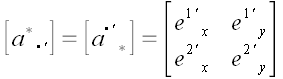 .
.
В новой системе координат вектор
 имеет координаты
имеет координаты
 .
Следовательно,
.
Следовательно,
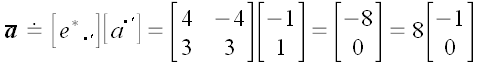 .
.
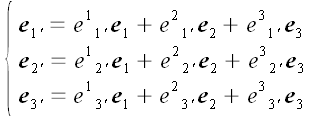 ;
;
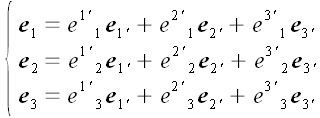 .
.
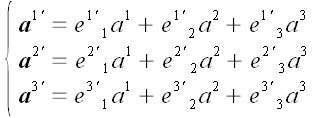
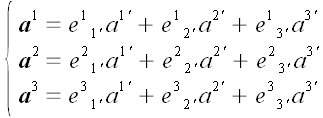
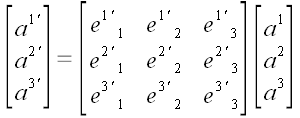 и
и
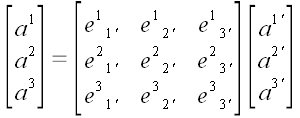 .
.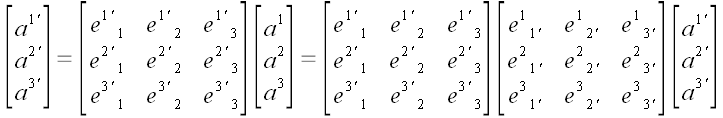 .
.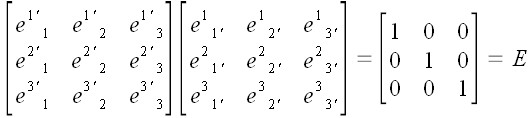 ,
где
,
где 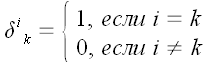 .
. ;
;
 .
.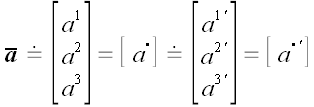 .
.
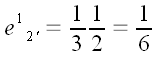 .
Аналогично
.
Аналогично
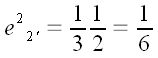 .
.
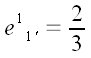 .
Проекция вектора
.
Проекция вектора
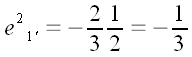 ;
;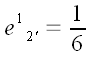 ;
;
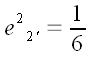 .
.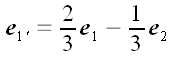 и
и
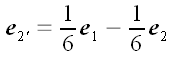 ;
;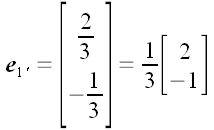 ;
;
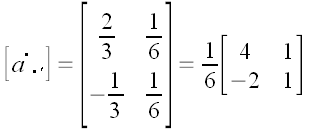 .
.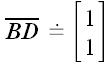 .
.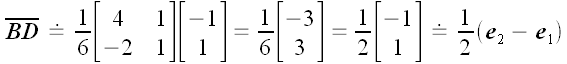 .
.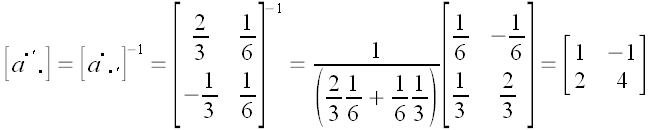 .
.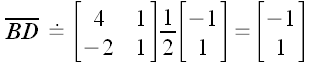 .
.
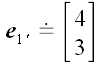 ,
,
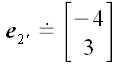 .
. .
.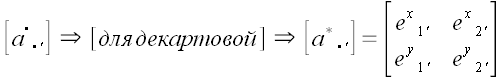 .
.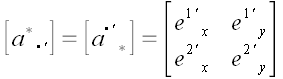 .
. .
Следовательно,
.
Следовательно,
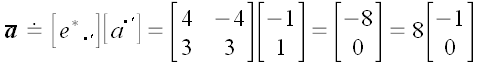 .
.