В.
Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Суперобложка /
Обложка /
Содержание

Базис,
состоящий из произвольной тройки некомпланарных векторов, принято
называть произвольной косоугольной системой координат. Такая система
неудобна для практических вычислений и не очень естественна. На
практике никто не измеряет длину в метрах, ширину в дюймах, а высоту
в лаптях. Если мы и пользуемся произвольной косоугольной системой
координат, то эта мера вынужденная. Например, даже если мы свяжем с
упругим телом какую-либо удобную для нас систему координат, то в
процессе деформации упругого тела эта система, мягко говоря,
покоробится. Есть проблемы, при изучении которых, мы принципиально не
можем воспользоваться какой-либо специальной системой координат.
В тех случаях, когда обстоятельства позволяют, и задача этого
требует, удобнее использовать некую специальную систему координат.
Таких систем изобретено достаточно много: цилиндрическая,
сферическая, полярная, эллиптическая и т.д. Очень часто оказывается
удобна так называемая декартовая система координат.
Декартовой называется система, базисные векторы которой взаимно
ортогональны, по модулю равны единице и образуют правую тройку.
Обозначаются базисные векторы латинскими буквами, которые называются,
в соответствии с традицией, по-французски: i – и,
j – жи, k – ка (рис. 14).
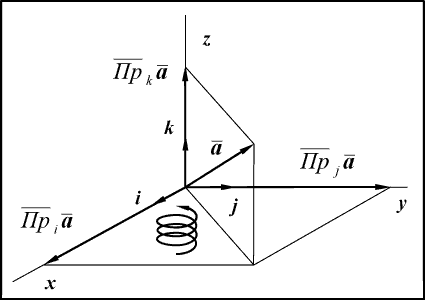 Рис. 14
Рис. 14
Правил, позволяющих отличить правую тройку векторов от левой, имеется
несколько. Из них наиболее часто используются четыре:
1. Правило левой руки.
Если кисть левой руки направить по направлению первого вектора и
расположить ее так, чтобы второй вектор был направлен в ладонь, и
если при этом большой палец левой руки будет направлен так же как
третий вектор, то векторы образуют правую тройку векторов.
2. Правило правого винта.
Если первый вектор поворачивать по кратчайшему расстоянию в сторону
второго, то третий вектор правой тройки векторов должен быть
направлен в ту же сторону, в которую при таком вращении будет
заворачиваться правый винт. Это правило на рис. 14
проиллюстрировано изображением спирали.
Остальные два правила не имеют названия.
3. Три вектора образуют правую тройку векторов, если при наблюдении
из конца третьего вектора вращение первого по кратчайшему расстоянию
в сторону второго происходит против часовой стрелки.
4. Если мы находимся внутри трехгранного угла, образованного тройкой
векторов, и если при этом поворот от первого вектора ко второму, а
затем к третьему должны выполнить против часовой стрелки, то векторы
образуют правую тройку векторов.
Можно предложить и еще одно правило:
5. Векторы
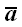 ,
,
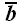 и
и
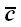 в указанном порядке образуют правую тройку векторов, если, будучи
выстроенными в том же порядке друг за другом, они образуют правую
спираль (рис. 15).
в указанном порядке образуют правую тройку векторов, если, будучи
выстроенными в том же порядке друг за другом, они образуют правую
спираль (рис. 15).
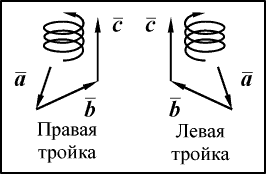 Рис. 15
Рис. 15
Наличие большого количества правил говорит о том, что все они не
очень удобны, и для того, чтобы научиться отличать правую тройку
векторов от левой, требуется определенная тренировка.
Вектор i (и) обычно совмещают с осью x,
вектор j (жи) – с осью y,
а вектор k (ка) – с осью z.
Поскольку базисные векторы декартовой системы координат взаимно
ортогональны, то координаты произвольного вектора в такой системе
совпадают с его ортогональными проекциями.
Пример обозначения координат произвольного вектора
 (рис. 14).
(рис. 14).
 ,
,
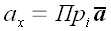 ;
;
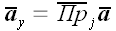 ,
,
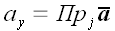 ;
;
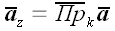 ,
,
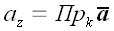 .
.
Следовательно, в декартовой системе координат произвольный вектор
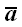 может быть представлен в виде:
может быть представлен в виде:
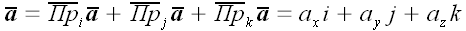 .
.
Модуль вектора
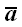 ,
как видно из рис. 14, вычисляется как корень квадратный из суммы
квадратов его координат:
,
как видно из рис. 14, вычисляется как корень квадратный из суммы
квадратов его координат:
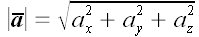 .
.
Если обозначить углы между вектором
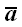 и векторами i, j и k
соответственно
и векторами i, j и k
соответственно
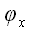 ,
,
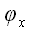 и
и
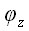 , то разложение вектора по векторам базиса запишется так:
, то разложение вектора по векторам базиса запишется так:
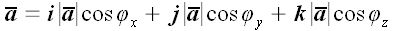 или
или
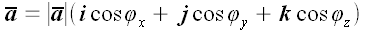 .
.
Вектор, совпадающий по направлению с вектором
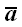 и имеющий единичную длину, называется направляющим вектором, или
ортом-вектором, или просто ортом. Орт-вектор обозначается обычно с
ноликом в правом верхнем углу:
и имеющий единичную длину, называется направляющим вектором, или
ортом-вектором, или просто ортом. Орт-вектор обозначается обычно с
ноликом в правом верхнем углу:
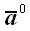 – орт-вектор вектора
– орт-вектор вектора
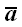 .
.
Так как
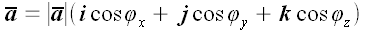 и
и
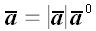 ,
то
,
то
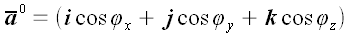 .
.
Косинусы в последнем выражении, которые являются координатами
орта-вектора, называются направляющими косинусами.
Вектор, проведенный из начала координат в некоторую точку M,
называется радиусом-вектором этой точки. Координаты точки (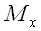 ,
,
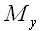 и
и
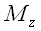 )
и координаты ее радиуса-вектора совпадают:
)
и координаты ее радиуса-вектора совпадают:
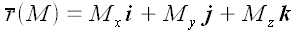 .
.
Если нам заданы в пространстве две точки
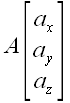 и
и
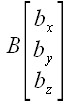 ,
то координаты вектора можно вычислить, воспользовавшись тем, что
,
то координаты вектора можно вычислить, воспользовавшись тем, что
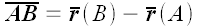 (рис.
16).
(рис.
16).
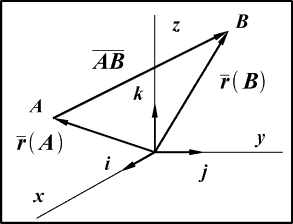 Рис. 16
Рис. 16
Выразив координаты
радиусов-векторов через координаты точек, мы получим:
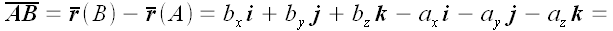
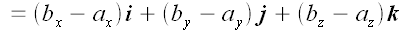 .
.
Следовательно, координаты вектора, проведенного из точки в A
точку B, равны разности соответствующих координат этих
точек.
.. Различные формы записи векторов
Принято различать координатную и векторную формы записи векторов. До
сих пор мы пользовались только векторной формой записи. Но если мы
выберем и зафиксируем в пространстве некоторую систему координат, то
для задания любого вектора нам будет достаточно задать его
координаты. Координаты, то есть три числа, взятые в определенном
порядке, однозначно определяют вектор в выбранной системе координат.
Поэтому можно записать:
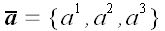 .
Слева в этом равенстве стоит вектор, следовательно, под таблицей
чисел, стоящей справа, необходимо понимать вектор с соответствующими
координатами. Такая форма записи часто используется в векторной
алгебре и называется координатной.
.
Слева в этом равенстве стоит вектор, следовательно, под таблицей
чисел, стоящей справа, необходимо понимать вектор с соответствующими
координатами. Такая форма записи часто используется в векторной
алгебре и называется координатной.
Таблицу
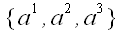 можно записать по-разному, например так, как это принято в матричной
алгебре:
можно записать по-разному, например так, как это принято в матричной
алгебре:
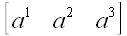 или
или
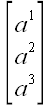 .
.
Если под этими таблицами также понимать вектор с соответствующими
координатами, то все эти таблицы представляют один и тот же вектор.
Значит, мы имеем право записать:
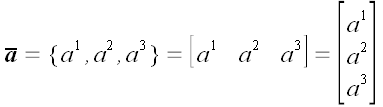 .
.
Если рассматривать это равенство, как векторное, то его следует
признать правильным. Однако, с точки зрения матричной алгебры,
таблицы
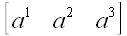 и
и
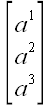 представляют собой различные матрицы, и между ними не может быть
поставлен знак равенства. Можно было бы проигнорировать эту проблему,
поскольку матричная алгебра является самостоятельной наукой и, если
не смешивать матричную и векторную алгебры, то недоразумений не
возникает. Кроме того, никто не заставляет использовать матричный
формат записи координат векторов. Общепринятой является форма записи
координат векторов в фигурных скобках, которая не используется в
теории матриц. Выходит, что, если ограничиться только общепринятой
формой, то проблем не возникает. Но дело все в том, что матричная и
векторная алгебры близки и по духу, и по решаемым проблемам. Когда
дело доходит до реальных вычислений с векторами, полезно использовать
матричные методы и обозначения. Короче говоря, матричную и векторную
алгебры полезно максимально интегрировать. Для
того, чтобы при этом возникало меньше проблем, мы слегка
модернизируем обозначения:
представляют собой различные матрицы, и между ними не может быть
поставлен знак равенства. Можно было бы проигнорировать эту проблему,
поскольку матричная алгебра является самостоятельной наукой и, если
не смешивать матричную и векторную алгебры, то недоразумений не
возникает. Кроме того, никто не заставляет использовать матричный
формат записи координат векторов. Общепринятой является форма записи
координат векторов в фигурных скобках, которая не используется в
теории матриц. Выходит, что, если ограничиться только общепринятой
формой, то проблем не возникает. Но дело все в том, что матричная и
векторная алгебры близки и по духу, и по решаемым проблемам. Когда
дело доходит до реальных вычислений с векторами, полезно использовать
матричные методы и обозначения. Короче говоря, матричную и векторную
алгебры полезно максимально интегрировать. Для
того, чтобы при этом возникало меньше проблем, мы слегка
модернизируем обозначения:
1. Обозначение точек
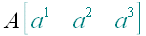 ,
или
,
или
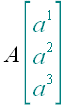 .
.
Точки будем обозначать большими буквами латинского алфавита. То, что
обведено зеленоватым цветом, является необязательной частью
обозначения. К необязательной части обозначения относится матрица с
координатами точки.
Примеры: A,
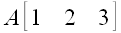 ,
,
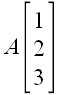 .
.
2. Обозначение векторов
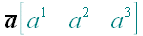 ,
,
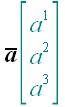 ,
,
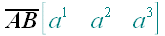 ,
,
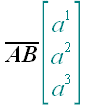 .
.
Примеры:
 ,
,
 ,
,
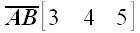 .
.
Кроме того, чтобы легче было переходить от векторов к матрицам и
наоборот, введем знак "соответствия"
"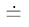 "
– знак "равно" с точкой наверху. Этим знаком мы будем
объединять одинаковые по смыслу векторные и матричные выражения,
например,
"
– знак "равно" с точкой наверху. Этим знаком мы будем
объединять одинаковые по смыслу векторные и матричные выражения,
например,
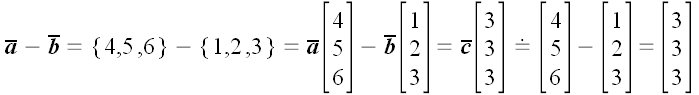 .
.
Прочитать это выражение можно так: "Разнице векторов слева
соответствует разность матриц справа".
Мы не будем давать точного определения для введенного нами знака
"соответствия", рассматривая его в качестве "осторожного"
знака равенства. Он должен напоминать, что хотя выражения,
объединенные им, в известной степени, равны по смыслу, следует
соблюдать осторожность при формальных преобразованиях.
..Линейные операции над векторами в координатной форме
Линейные операции над векторами можно выполнять как в векторной, так
и в координатной формах, например:
1. Сложение векторов.
Векторная форма.
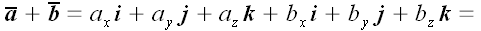
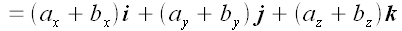 .
.
Координатная форма.
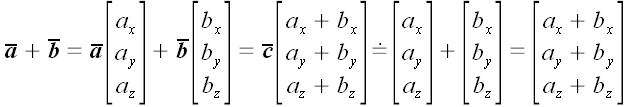 .
.
2. Умножение вектора на число.
Векторная форма.
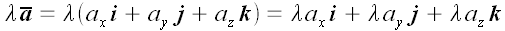 .
.
Координатная форма.
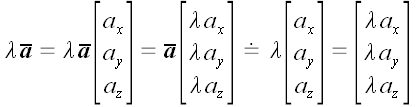 .
.



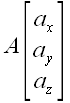 и
и
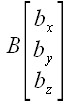 ,
то координаты вектора можно вычислить, воспользовавшись тем, что
,
то координаты вектора можно вычислить, воспользовавшись тем, что
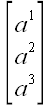 .
.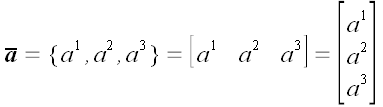 .
.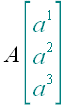 .
. .
.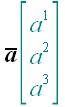 ,
,
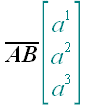 .
.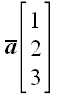 ,
,
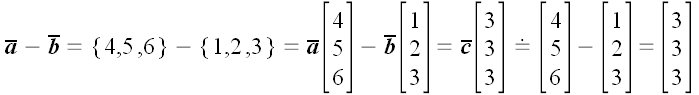 .
.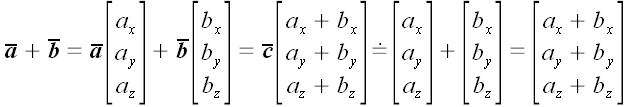 .
.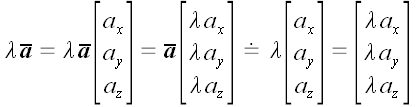 .
.