В.
Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Суперобложка /
Обложка /
Содержание

Для
того чтобы научиться свободно выполнять преобразования с тензорными
величинами, необходима тренировка. Особенно полезно как можно больше
прорешать задач на тождественные преобразования. К сожалению,
специальных задачников по тензорной алгебре не существует. Тем не
менее, задачи найти можно: каждый автор учебника обязательно их
приводит. Конечно, в учебниках задач не бывает слишком много, но к
счастью самих учебников по теории тензоров порядочно. Другая
возможность заключается в том, чтобы применять тензорный аппарат для
доказательства известных фактов, где это только возможно. Несколько
задач такого типа мы здесь приводим.
..Задачи на тождественные преобразования
1. В векторной алгебре доказывается формула для двойного векторного
произведения
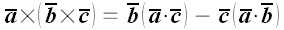 ,
которую для запоминания иногда называют формулой "Бац минус
Цаб". К сожалению, это название мало помогает. Стоит только
иначе расставить скобки, и мы получим:
,
которую для запоминания иногда называют формулой "Бац минус
Цаб". К сожалению, это название мало помогает. Стоит только
иначе расставить скобки, и мы получим:
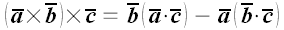 .
А если для обозначения векторов использовать другие буквы или иначе
их расставить, то о названии "Бац
минус Цаб" лучше совсем не вспоминать.
.
А если для обозначения векторов использовать другие буквы или иначе
их расставить, то о названии "Бац
минус Цаб" лучше совсем не вспоминать.
Формула, тем не менее, полезная и часто используется. Для того чтобы
при любых вариантах ее правильно воспроизвести, достаточно запомнить,
что двойное векторное произведение раскладывается по векторам,
заключенным в скобки:
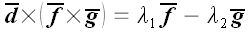 .
Причем в этом разложении со знаком плюс идет всегда средний вектор, а
со знаком минус – другой. Скалярные произведения оставшихся
векторов образуют коэффициенты этого разложения:
.
Причем в этом разложении со знаком плюс идет всегда средний вектор, а
со знаком минус – другой. Скалярные произведения оставшихся
векторов образуют коэффициенты этого разложения:
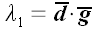 ,
,
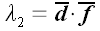 .
И мы получаем, что
.
И мы получаем, что
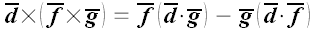 .
.
Докажем формулу
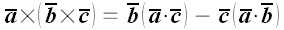 ,
используя индексную форму записи, принятую в тензорной алгебре в
качестве основной.
,
используя индексную форму записи, принятую в тензорной алгебре в
качестве основной.
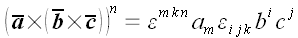 .
.
Свернем тензоры Леви-Чивиты.
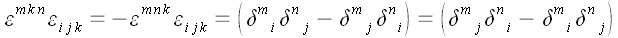 .
.
Далее получаем:
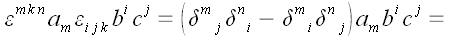
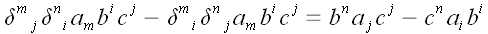 .
.
Полученное выражение как раз и является выражением исходной формулы в
координатной форме.
2. Доказать тождество Лагранжа
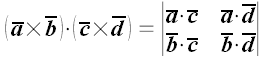 .
.
Решение
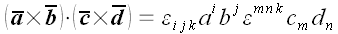 ;
;
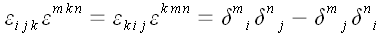 ;
;
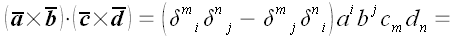
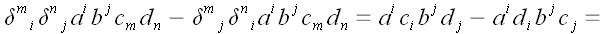
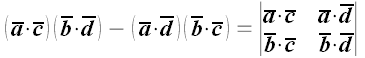
3. Доказать формулу
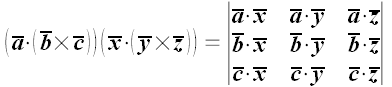
Решение
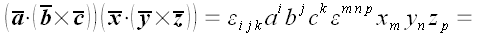
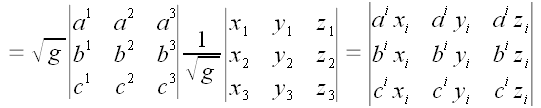
Следовательно:
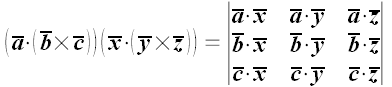 .
.
Что и требовалось доказать.
Остальные задачи предлагаются для самостоятельного решения.
4. Доказать тождество Лагранжа
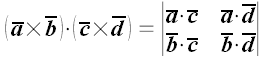 .
.
5. Доказать тождество Якоби
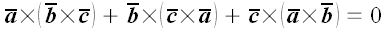 .
.
6. Найти
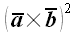 и записать в координатной форме.
и записать в координатной форме.
7. Доказать, что из равенства
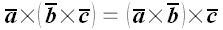 .
.
следует коллинеарность векторов
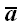 и
и
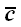 ,
если
,
если
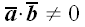 и
и
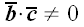 .
.
8. Вычислить смешанное произведение
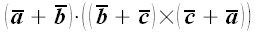 .
.
9. Доказать формулы:
а)
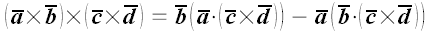
б)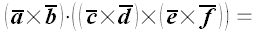
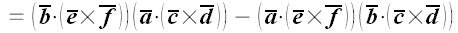 .
.
10. Доказать, что
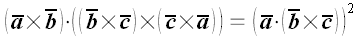 .
.
11. Доказать формулу
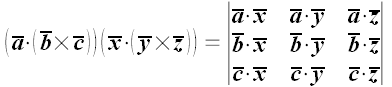 .
.
.О возникновении терминологии и обозначений,
используемых в векторном исчислении
Даже
при беглом знакомстве с предметом нельзя не заметить известную
избыточность обозначений и специальных значков в векторной и
тензорной алгебрах. Данная проблема сложилась не сегодня. Феликс
Клейн в своей книге "Элементарная математика с точки зрения
высшей" 1925-ого г. издания приводит
интересный материал об истории и о причинах возникновения этой
проблемы.
"Мне хочется прибавить несколько слов по поводу прискорбного
вопроса о системе обозначений в векторном анализе. Дело в том, что
для каждого действия с векторами употребляется большое количество
различных знаков, и, к сожалению, до сих пор еще не удалось создать
одну-единственную общеобязательную систему обозначений. Четыре года
назад на съезде естествоиспытателей в Касселе (1903) с этой целью
была даже избрана специальная комиссия, но члены ее не смогли вполне
столковаться, а так как каждый из них все же имел доброе желание
сделать шаг от своей первоначальной точки зрения навстречу другим
взглядам, то единственным результатом явилось возникновение трех
новых обозначений! После этого и других аналогичных случаев я пришел
к тому заключению, что действительное объединение всех
заинтересованных в таких вещах кругов на почве одних и тех же
словесных и письменных обозначений возможно только в тех случаях,
когда к этому побуждают в высшей степени важные материальные
интересы. Только под таким давлением могло произойти в 1881г. в
электротехнике признание единообразной системы мер вольт –
ампер – ом и последующее закрепление ее государственным
законодательством, так как промышленность настойчиво требовала
подобного единства мер как основы всех операций. За векторным
исчислением еще не стоят такие могущественные материальные стимулы, и
поэтому приходится пока что – плохо ли, хорошо ли –
мириться с тем, что каждый отдельный математик остается при привычном
для него способе обозначений, который он считает наиболее удобным
или даже – если он несколько склонен к догматизму –
единственно правильным".
"...на конгрессе математиков в Риме (1908) избрали
интернациональную комиссию, которая должна была предложить единую
систему обозначений. ...
Созданная комиссия по унификации векторных обозначений не имела, как
и следовало ожидать, ни малейшего успеха. На следующем
интернациональном конгрессе в Кембридже (1912) она вынуждена была
объявить, что не успела закончить своих работ, и просить о продлении
ее мандата до следующего конгресса, который должен был собраться в
1916 г. в Стокгольме, но не состоялся из-за войны. Такая же судьба,
по-видимому, постигнет и "Комиссию единиц и величин, входящих в
формулы". Последняя опубликовала в 1921 г. проект обозначения
векторных величин и вызвала этим тотчас же самые резкие возражения с
различных сторон.
Общеупотребительная теперь терминология векторного исчисления
исторически возникла главным образом из двух источников: из
гамильтонова исчисления кватернионов и из грассманова учения о
протяжении.
...
В связи с тем, что ортодоксальные во всем прочем последователи
Грассмана заменили очень целесообразные обозначения учителя отчасти
другими, а физики смешали воедино, либо модифицировали имеющиеся
терминологии, а также проявили крайне большой произвол по отношению к
знакам отдельных операций, получается, наконец, даже для специалиста
большая неразбериха в этой математически совершенно простой области".
Мы привели эту развернутую цитату потому, что она удивительно точно
характеризует проблему с обозначениями и определениями понятий в
современных векторной и тензорной алгебрах. Отмеченная Ф. Клейном
неразбериха в этих очень полезных для физиков и инженеров
математических теориях благополучно доползла до наших дней через
столетие.
.Проекция вектора на ось
Понятие
проекции вектора на ось является одним из самых простых и полезных
для приложений. Именно поэтому вызывает недоумение имеющая место
несогласованность этого понятия в векторной алгебре с более общим
понятием проекции. Видимо, стремлением преодолеть эту
несогласованность, с одной стороны, и нежеланием слишком долго
задерживаться на этом ровном месте, с другой стороны, можно как-то
объяснить возникшую при этом путаницу.
По определению, которого придерживается большинство авторов, проекция
вектора на ось – это число. Но это нелогично. Проекция точки
есть точка, проекция отрезка есть отрезок, проекция вектора на
плоскость есть вектор, даже проекция вектора на прямую есть, по
мнению некоторых авторов, вектор, а проекцией вектора на ось является
число. Такое определение видимо связано с тем фактом, что в
декартовой системе координат произвольный вектор a
может быть представлен в виде:
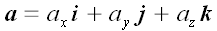 ,
где
,
где
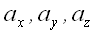 –
числа, которые по существующей традиции принято называть проекциями
вектора. Векторы
–
числа, которые по существующей традиции принято называть проекциями
вектора. Векторы
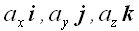 называются составляющими или компонентами вектора a.
называются составляющими или компонентами вектора a.
Определение проекции вектора как числа получило широкое
распространение, и, будучи изначально нелогичным, и породило
упомянутую путаницу.
Приведу несколько цитат с комментариями.
"Нельзя отождествлять понятия проекции силы и ее составляющей.
... Составляющая силы является вектором, который можно представить в
виде произведения проекции силы на орт соответствующей оси" [3,
с. 34].
Слово "составляющая" здесь является точным переводом
англоязычного термина "компонента". В дальнейшем мы не
будем эти термины различать, как, впрочем, и авторы задачника по
высшей математике, цитату из которого я привожу ниже.
"Векторы
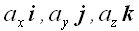 в виде суммы которых представлен вектор a,
называются составляющими (компонентами) вектора a
по осям координат" [6, с. 45].
в виде суммы которых представлен вектор a,
называются составляющими (компонентами) вектора a
по осям координат" [6, с. 45].
Следующая цитата из учебника по теоретической механике.
"Рассмотрим вектор
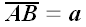 и ось Ох, не лежащие, в общем случае, в одной плоскости.
Проведем через точки А и В две плоскости,
перпендикулярные к Ох и отметим точки а и b
их пересечения с осью Ох. Как известно, отрезку ab
можно поставить в соответствие положительное число, если направление
этого отрезка совпадает с положительным направлением оси Ох, и
отрицательное, если направление отрезка ab
и оси Ох противоположны. Этот отрезок или соответствующее ему
число будем называть проекцией вектора
и ось Ох, не лежащие, в общем случае, в одной плоскости.
Проведем через точки А и В две плоскости,
перпендикулярные к Ох и отметим точки а и b
их пересечения с осью Ох. Как известно, отрезку ab
можно поставить в соответствие положительное число, если направление
этого отрезка совпадает с положительным направлением оси Ох, и
отрицательное, если направление отрезка ab
и оси Ох противоположны. Этот отрезок или соответствующее ему
число будем называть проекцией вектора
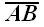 на ось Ох" [8, с. 29-30].
на ось Ох" [8, с. 29-30].
Здесь, по сути, даны два определения: проекции как вектора
(направленный отрезок ab) и как
скаляра (соответствующее ему число). Но автор не вводит различные
обозначения для разных случаев, что в дальнейшем приводит к
неоднозначности в прочтении текста.
Следующие выдержки приводятся из известного учебника по общему курсу
физики И.В. Савельева.
"Величина
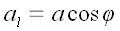 (а – модуль вектора) называется проекцией вектора а
на ось l.
(а – модуль вектора) называется проекцией вектора а
на ось l.
...
...вектор а можно представить в виде линейной
комбинации ортов
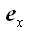 и
и
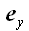 :
:
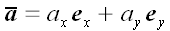 .
Роль коэффициентов при этом играют проекции вектора на оси координат.
.
Роль коэффициентов при этом играют проекции вектора на оси координат.
...
Таким образом, любой вектор можно выразить через его проекции на
координатные оси и орты этих осей. В связи с этим проекции на
координатные оси называются компонентами вектора" [15,
с. 22-23]. Подчеркнуто мной. Получается, что, с одной стороны,
проекции вектора на координатные оси являются числами, но, с другой
стороны, они являются компонентами вектора и поэтому должны считаться
векторами.
Для практических целей важны оба понятия: и понятие компоненты, и
понятие проекции вектора на ось. Но нелогичное определение одного из
них приводит к терминологической путанице. Следующий автор пытается
развести эти понятия.
"Не следует отождествлять проекцию вектора на ось и проекцию
вектора на прямую. В первом случае – это число, а во втором –
вектор" [14, с. 93].
Следовательно, если мы хотим получить вектор, мы должны считать, что
проектируем вектор на прямую. Если же нам хочется иметь число, надо
проектировать вектор на ось. Вряд ли это удобно, и кроме
дополнительной путаницы ничего не дает.
Наиболее решительно и последовательно разводит эти понятия
Г.Ф. Лаптев [12, с. 33]. Для этого ему
приходится вводить два вида проекции вектора на ось: скалярную и
векторную.
"Векторной проекцией вектора на ось называется вектор, началом
и концом которого являются соответственно проекция начала и проекция
конца исходного вектора на данную ось.
Векторная проекция вектора a на ось s
обозначается
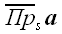 или
или
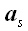 :
:
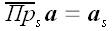 .
.
...
Проекцией или скалярной проекцией вектора на ось
называется скаляр, абсолютная величина которого равна модулю
векторной проекции того же вектора на ту же ось. При этом проекция
считается положительной, если направление векторной проекции
совпадает с направлением оси, и отрицательной в противном случае.
Скалярная проекция вектора a
на ось s обозначается
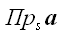 или
или
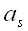 :
:
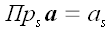 ".
".
Ну вот, казалось бы, и все – проблема решена. Вместо одной
скалярной проекции мы имеем две: векторную, что логично, и скалярную,
что удобно и привычно. К сожалению, проблема серьезнее. При
определении проекции вектора традиционно имеется ввиду параллельная
ортогональная проекция, хотя об этом не принято говорить явно. Пока
мы находимся в декартовой системе координат, такое предпочтение
выглядит естественно. Но стоит только перейти к произвольному базису
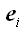 ,
как в разложении вектора a по
координатным осям
,
как в разложении вектора a по
координатным осям
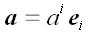 коэффициенты
коэффициенты
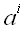 уже не могут считаться проекциями в вышеуказанном смысле. Как
результат, в тех курсах векторной алгебры, в которых авторы не
ограничиваются только декартовой системой координат, понятие проекции
вектора на ось либо не используется вовсе, либо имеет ограниченное
применение. А зря, ведь типичное в таких случаях определение
координаты вектора как некоего коэффициента в разложении по векторам
базиса неконструктивно, так как не указывает способа вычисления этого
коэффициента. Определение же координаты вектора через проекцию,
напротив, конструктивно. Надо только отказаться от узкого определения
проекции вектора на ось, как от ортогональной проекции, и перейти к
более широкому классу параллельных проекций. Но для задания
параллельной проекции уже недостаточно знать только ось или
плоскость, на которую производится проектирование, необходимо еще
задать направление проектирования. В связи с этим требуется
модернизировать обозначение для проекции вектора на плоскость и на
ось.
уже не могут считаться проекциями в вышеуказанном смысле. Как
результат, в тех курсах векторной алгебры, в которых авторы не
ограничиваются только декартовой системой координат, понятие проекции
вектора на ось либо не используется вовсе, либо имеет ограниченное
применение. А зря, ведь типичное в таких случаях определение
координаты вектора как некоего коэффициента в разложении по векторам
базиса неконструктивно, так как не указывает способа вычисления этого
коэффициента. Определение же координаты вектора через проекцию,
напротив, конструктивно. Надо только отказаться от узкого определения
проекции вектора на ось, как от ортогональной проекции, и перейти к
более широкому классу параллельных проекций. Но для задания
параллельной проекции уже недостаточно знать только ось или
плоскость, на которую производится проектирование, необходимо еще
задать направление проектирования. В связи с этим требуется
модернизировать обозначение для проекции вектора на плоскость и на
ось.
.Определитель
Понятие
определителя традиционно связывается с решением систем линейных
уравнений и правилами Крамера. Однако давно уже признано, что роль
определителей в практике решения систем линейных уравнений сильно
преувеличена. В то же время геометрический смысл определителя
отражен, по нашему мнению, во многих учебниках по высшей математике
недостаточно. Не следует, конечно, полностью отказываться от
традиций, но сделать определенный акцент в сторону геометрии на наш
взгляд было бы полезно.
.Векторное произведение
Для
введения векторного умножения имеются две равнозначные возможности и
обе эти возможности, как обычно и бывает в таких случаях,
используются. Ряд авторов определяет векторное произведение как
истинный, абсолютный или полярный вектор, связывая его направление с
направлением правого винта [1, 5,
12]. Другие же предпочитают связывать его
направление с текущей системой координат, получая при этом псевдо или
аксиальный вектор [7, 8,
11, 14]. Речь в
данном случае идет о близких, но, тем не менее различных
математический объектах, одинаково пригодных для отражения свойств
таких геометрических и физических величин, как угловая скорость,
угловое ускорение, момент силы, момент пары сил и т.д. Несмотря на
то, что разница между двумя определениями векторного умножения чисто
символическая, вторая возможность нам представляется более
адекватной, поскольку само определение подчеркивает условный характер
направление этих величин.
.Символ Кронекера
В
отношении символа Кронекера есть две диаметрально противоположные
точки зрения. Согласно одной из них – это просто символ и
положение индексов (верхнее или нижнее) для него не имеет значения
[7]. Согласно другой, символ Кронекера
является абсолютным тензором [18]. Но если
принять символ Кронекера за абсолютный тензор, то он становится
полностью эквивалентен метрическому тензору и это делает его
излишним.
.Символ Веблена
Символы
подобные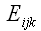 вводят многие авторы, к сожалению, под разными названиями. Например,
М.А. Акивис [1] называет их кососимметричными символами
Кронекера, И. Сокольников [18] –
e-системой. Мы назвали эти символы
символами Веблена вслед за В.И. Блохом [5].
К сожалению, В.И. Блох никак не называет букву необычного
начертания, которую он использует для обозначения символов Веблена, и
не дает необходимых комментариев для того, чтобы ее можно было
однозначно отнести к какому-то алфавиту. Поэтому мы вынуждены были
использовать наше обозначение, которое, естественно не является
общепринятым. Теме не менее мы считаем, что оно вполне обосновано, и
в той или иной степени сходно с обозначениями принятыми
М.А. Акивисом, И. Сокольниковым, В.И. Блохом и
некоторыми другими авторами.
вводят многие авторы, к сожалению, под разными названиями. Например,
М.А. Акивис [1] называет их кососимметричными символами
Кронекера, И. Сокольников [18] –
e-системой. Мы назвали эти символы
символами Веблена вслед за В.И. Блохом [5].
К сожалению, В.И. Блох никак не называет букву необычного
начертания, которую он использует для обозначения символов Веблена, и
не дает необходимых комментариев для того, чтобы ее можно было
однозначно отнести к какому-то алфавиту. Поэтому мы вынуждены были
использовать наше обозначение, которое, естественно не является
общепринятым. Теме не менее мы считаем, что оно вполне обосновано, и
в той или иной степени сходно с обозначениями принятыми
М.А. Акивисом, И. Сокольниковым, В.И. Блохом и
некоторыми другими авторами.
.Об обозначениях
Нет
ничего практичнее хорошей теории. Говорят, этот афоризм придумал
Нильс Бор. Но практичность любой теории прямо пропорциональна
полезному результату от ее применения и обратно пропорциональна
затратам на ее изучение.
Возможно не будет преувеличением, если сказать, что львиная доля
затрат на изучение любой теории связана с изучением ее специфического
языка и связанной с ним письменностью. Математическая письменность в
какой-то степени аналогична китайской грамоте. По крайней мере,
различных значков, которые в ней используются, не меньше, чем
китайских иероглифов. Хорошо если введение нового значка хоть как-то
оправдано, но это бывает не всегда. Просматривая книги по векторной и
тензорной алгебре, мы нашли, что разные авторы для обозначения
матрицы преобразования использовали следующие обозначения:
A,
B, C,
a, b,
Γ,
γ,
e,
h,
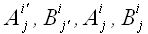 ,
,
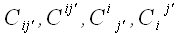 ,
,
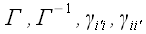 ,
,
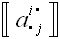 ,
,
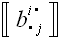 ,
,
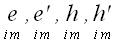 .
Всего, если не учитывать индексов в различных вариантах, для
обозначения матрицы преобразования были использованы следующие
символы: A, B, C, a, b, Γ,
γ,
e,
h.
В разных книгах для обозначения векторов базиса используются
следующие символы: э, e, h,
a, b, α, β. Зачем, если есть
общеупотребительное
.
Всего, если не учитывать индексов в различных вариантах, для
обозначения матрицы преобразования были использованы следующие
символы: A, B, C, a, b, Γ,
γ,
e,
h.
В разных книгах для обозначения векторов базиса используются
следующие символы: э, e, h,
a, b, α, β. Зачем, если есть
общеупотребительное
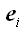 ?
?
Может показаться, что проблема обозначений мало существенная. В самом
деле, какая разница, как мы обозначили ту или иную величину, если мы
подробно при этом ее описали. Но если обозначение никак не связано с
содержанием, то для понимания дальнейшего текста ее придется просто
запомнить. И чем меньше смысла в обозначении, тем труднее его
запомнить. Поэтому, самым лучшим обозначением является "говорящее",
которое что-то подсказывает, упрощая либо само запоминание, либо
выполнение каких-то действий с обозначенной величиной.
Выбор алфавита, из которого выбран символ, также имеет значение.
Например, Хевисайд считал, что уже одно то, что Максвелл обозначал
векторы готическими буквами, может вызвать предубеждение читателя
против векторного анализа.
Конечно, невозможно тщательно продумать каждое обозначение и при
изложении любой теории невозможно обойтись без множества
промежуточных случайных обозначений. Но хотя бы для тех величин,
которые в данной теории играют фундаментальную роль, хотелось бы
видеть простые, ясные и удобные для запоминания значки.
.Требования к определениям математических понятий
"Назначение
определений в том и состоит, что они подытоживают главное в
исследовании предмета" [21, с. 148].
Дать определение, правильно отражающее сущность предмета, на раннем
этапе его исследования не представляется возможным. Иногда на
протяжении многих лет, а иногда даже столетий приходится пользоваться
неполными или даже неправильными определениями.
Считается, что правильное определение, вскрывающее сущность предмета,
может быть только одно [21, с. 149].
Возможно, что так оно и есть и возможно так оно и будет, когда наука
закончится, и для каждого понятия будет, наконец, дано единственное
полное и правильное определение. К счастью наука еще очень далека от
завершения.
В большинстве математических учебников определения чаще всего
возникают только по воле их творцов на совершенно ровном месте
абсолютно из ничего, как кролик из шляпы фокусника.
Например, в учебнике Л.И. Головиной по линейной алгебре дается
такое определение сопряженного оператора:
"Пусть A – линейное преобразование евклидова пространства
R. Линейное преобразование A, такое, что
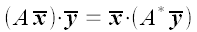 при всех
при всех
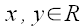 ,
называется сопряженным к A".
,
называется сопряженным к A".
Что это определение определяет? Зачем оно понадобилось? Для чего
необходимо выделять преобразование с указанным свойством? В каком
отношении вновь определяемый объект находится с теми математическими
объектами, которые были введены ранее. В учебниках по математике
редко останавливаются на этих вопросах. Но для не математиков
математика интересна лишь в той степени, в которой она для них
полезна. А полезной для инженеров и физиков математика является лишь
в той степени, в которой она является наукой о всеобщих законах
природы. Математика как формальная система правил по формальным
преобразованиям предложений составленных из математических значков
инженерам не интересна.
Мы считаем, но конечно не настаиваем, что, придумывая определения
математических понятий для инженеров, физиков и других пользователей,
полезно следовать некоторым рекомендациям. Некоторые из таких
рекомендаций мы позволили себе сформулировать.
(1) Перед тем, как давать определение нового понятия, необходимо каким-то
образом показать его необходимость.
(2) Определение должно увязывать вновь вводимое понятие с теми, которые
уже хорошо изучены к настоящему моменту.
(3) Определение раскрывает сущность предмета и отличие его от других
предметов.
(4) Хорошо если определение математического понятия сформулировано таким
образом, что позволяет легко увидеть связь между ним и теми
геометрическими, физическими и техническими объектами, свойства
которых оно отражает.
(5) Определение должно быть удобным для использования в конкретной теории
при решении ее специфических задач.
(6) Название понятия должно по возможности правильно отражать его
содержание.
(7) Определение по возможности должно быть простым, кратким и удобным для
обобщения.
Трудно представить, что каждое определение может отвечать всем этим
требованиям, в особенности, если учесть, что оно обязано быть простым
и кратким. Отсюда вытекает еще одна рекомендация:
(8) лучше если определений будет несколько, причем каждое из них будет
по-своему удобным и ясным.
.Определение тензора
П.К. Рашевский дает следующее определение тензора [13].
Мы говорим, что нам задан
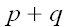 - валентный тензор,
- валентный тензор,
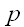 раз ковариантный и
раз ковариантный и
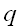 раз контравариантный, если в каждой координатной системе нам заданы
раз контравариантный, если в каждой координатной системе нам заданы
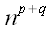 чисел
чисел
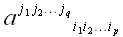 ,
занумерованных
,
занумерованных 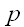 индексами внизу и
индексами внизу и 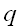 индексами наверху и преобразующихся при переходе от одной
координатной системы к другой по закону
индексами наверху и преобразующихся при переходе от одной
координатной системы к другой по закону
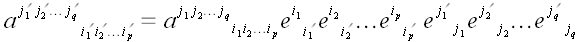 .
.
Числа
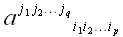 мы будем называть координатами тензора в соответствующей координатной
системе. Все индексы пробегают значения 1, 2, 3 ..., n
независимо друг от друга.
мы будем называть координатами тензора в соответствующей координатной
системе. Все индексы пробегают значения 1, 2, 3 ..., n
независимо друг от друга.
Данное определение тензора изящным образом уходит от ответа на
вопрос, что такое тензор. Можно только предположить, что тензор это
нечто, что определяется в каждой координатной системе определенным
набором чисел
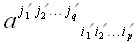 .
Обычно так и говорят, что тензор – это геометрический или
физический объект, который может быть задан своими координатами в
каждой координатной системе. Но что мы понимаем под геометрическим
объектом? Давайте попробуем перечислить: шар, пирамида, конус,
поверхность, трапеция... Что общего во всех этих объектах? Все они
имеют форму. Все геометрические объекты имеют форму. Физические
объекты обладают большим разнообразием, но и о многих из них можно
сказать то же самое. Поэтому, когда мы говорим студенту, что мы
определили геометрический или физический объект, он автоматически
пытается его представить. Но из всех по-настоящему геометрических, то
есть тех, что имеют форму, объектов только векторы удовлетворяют
приведенному определению. Даже геометрическая точка не может
считаться геометрическим объектом, поскольку ее координаты при
перемене базиса изменяются по другому закону. Следующие по сложности
объекты, которые могут быть заданы своими координатами, являются
линейные преобразования. Но линейные преобразования не имеют формы,
это просто функции, их нельзя представить в виде какого-то
геометрического объекта. То же самое можно сказать и обо всех
тензорах более сложного строения. Все это может показаться мало
существенным, однако это не так. Язык математики, так же как и язык
любой другой науки, не является полностью самостоятельным языком. Он
является расширением естественного языка и должен, поэтому, быть
максимально с ним согласован. Настоящее определение и другие подобные
ему постоянно провоцируют людей на бесплодные разговоры о том, что
такое тензор и как его представить. Те же, кто от бессмысленных
попыток "увидеть" тензор устает, навсегда отказываются от
надежды понять эту теорию.
.
Обычно так и говорят, что тензор – это геометрический или
физический объект, который может быть задан своими координатами в
каждой координатной системе. Но что мы понимаем под геометрическим
объектом? Давайте попробуем перечислить: шар, пирамида, конус,
поверхность, трапеция... Что общего во всех этих объектах? Все они
имеют форму. Все геометрические объекты имеют форму. Физические
объекты обладают большим разнообразием, но и о многих из них можно
сказать то же самое. Поэтому, когда мы говорим студенту, что мы
определили геометрический или физический объект, он автоматически
пытается его представить. Но из всех по-настоящему геометрических, то
есть тех, что имеют форму, объектов только векторы удовлетворяют
приведенному определению. Даже геометрическая точка не может
считаться геометрическим объектом, поскольку ее координаты при
перемене базиса изменяются по другому закону. Следующие по сложности
объекты, которые могут быть заданы своими координатами, являются
линейные преобразования. Но линейные преобразования не имеют формы,
это просто функции, их нельзя представить в виде какого-то
геометрического объекта. То же самое можно сказать и обо всех
тензорах более сложного строения. Все это может показаться мало
существенным, однако это не так. Язык математики, так же как и язык
любой другой науки, не является полностью самостоятельным языком. Он
является расширением естественного языка и должен, поэтому, быть
максимально с ним согласован. Настоящее определение и другие подобные
ему постоянно провоцируют людей на бесплодные разговоры о том, что
такое тензор и как его представить. Те же, кто от бессмысленных
попыток "увидеть" тензор устает, навсегда отказываются от
надежды понять эту теорию.
Но давайте вернемся к определению. Надо признать, что научный язык
часто изменяет первоначальный смысл слов естественного языка. В
качестве расширения понятия геометрического объекта, линейный
оператор, с известной натяжкой, может быть назван геометрическим
объектом, поскольку он один геометрический объект (вектор)
преобразует в другой геометрический объект. В соответствии с
определением будем считать, что линейный оператор, координатами
которого являются числа
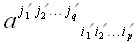 ,
как раз и есть тот тензор, о котором говорится в определении. Но в
этом случае возникает вопрос, какой именно оператор мы должны считать
тем тензором, который задан. Дело в том, что один и тот же набор
координат может порождать принципиально разные операторы. Например,
,
как раз и есть тот тензор, о котором говорится в определении. Но в
этом случае возникает вопрос, какой именно оператор мы должны считать
тем тензором, который задан. Дело в том, что один и тот же набор
координат может порождать принципиально разные операторы. Например,
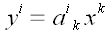 преобразует вектор
преобразует вектор
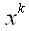 в вектор
в вектор
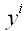 ,
а
,
а
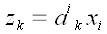 преобразует тот же вектор
преобразует тот же вектор
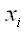 в другой вектор
в другой вектор
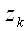 .
Тензоры более сложного строения предоставляют гораздо больше
возможностей для порождения различных операторов, имеющих одно общее
свойство – одинаковые координаты во всех координатных системах.
.
Тензоры более сложного строения предоставляют гораздо больше
возможностей для порождения различных операторов, имеющих одно общее
свойство – одинаковые координаты во всех координатных системах.
Приведенные обстоятельства привели нас к убеждению, что тензором
удобнее считать не геометрический объект (читай линейный оператор), а
его координаты. Набор чисел, массив, рассматриваемый как единый
математический объект с определенными свойствами – это и есть
тензор в нашем понимании. Отсюда, в частности, следует вывод, что
тензоры существуют только в связи с координатными системами. Этот
вывод, кстати, не противоречит и приведенному определению
П.К. Рашевского.
Наиболее яркое выражение альтернативной точки зрения на тензор как на
абсолютный, то есть независимый от конкретных координатных систем,
объект связано с так называемыми диадными и полиадными его
представлениями. Диада, так же как и полиада, представляет собой
искусственную композицию, составленную из векторов. Пусть
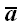 и
и
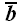 два произвольных вектора. Совокупности их координат являются
тензорами. Тензором также является их тензорное произведение
два произвольных вектора. Совокупности их координат являются
тензорами. Тензором также является их тензорное произведение
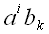 .
Этот тензор порождает линейный оператор
.
Этот тензор порождает линейный оператор
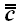 с матрицей координат
с матрицей координат
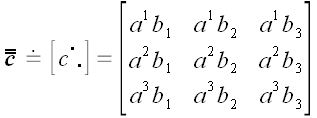 .
.
Найдем воздействие этого оператора на произвольный вектор
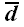 .
.
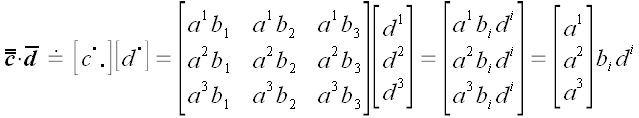 .
.
Этот результат короче можно записать в векторном виде
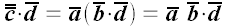 .
.
Два рядом записанные векторы
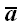 и
и
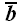 в последнем выражении называются диадой и считаются условным
обозначением для порожденного ими оператора
в последнем выражении называются диадой и считаются условным
обозначением для порожденного ими оператора
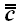 ,
следовательно,
,
следовательно,
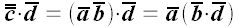 .
.
Аналогичным образом могут быть построены диады из векторов базиса.
Например, диада
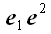 является линейным оператором, который произвольный вектор
является линейным оператором, который произвольный вектор
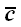 преобразует в вектор
преобразует в вектор
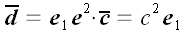 .
.
Матрица координат этого оператора:
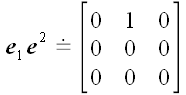 .
.
Поскольку матрица координат произвольного линейного оператора
 может быть представлена как
может быть представлена как
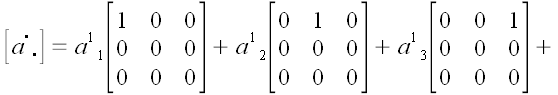
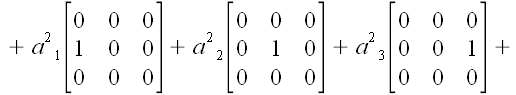
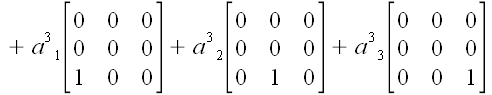 ,
,
то, используя базисные диады, мы можем записать, что
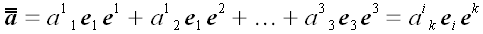 .
.
Искусственная конструкция
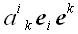 в этом выражении является условным обозначением оператора
в этом выражении является условным обозначением оператора
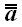 .
Для того, чтобы найти воздействие оператора
.
Для того, чтобы найти воздействие оператора
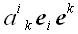 на произвольный вектор
на произвольный вектор
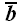 достаточно формально выполнить скалярное умножение:
достаточно формально выполнить скалярное умножение:
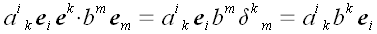 .
.
Аналогичным образом могут быть построены и более сложные формальные
математические структуры, например,
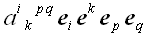 ,
которые по странному стечению обстоятельств принято называть
истинными тензорами, а также геометрическими или физическими
объектами. Последнее обстоятельство вызывает у людей определенные
психологические трудности аналогичные тем, о которых мы уже
упоминали. Вместе с тем данное направление обладает рядом достоинств,
связанных прежде всего с привычным векторным формализмом, и на
сегодняшний день настойчиво развивается. Более подробно об этом можно
посмотреть в соответствующей литературе [5,
16, 17].
,
которые по странному стечению обстоятельств принято называть
истинными тензорами, а также геометрическими или физическими
объектами. Последнее обстоятельство вызывает у людей определенные
психологические трудности аналогичные тем, о которых мы уже
упоминали. Вместе с тем данное направление обладает рядом достоинств,
связанных прежде всего с привычным векторным формализмом, и на
сегодняшний день настойчиво развивается. Более подробно об этом можно
посмотреть в соответствующей литературе [5,
16, 17].
При
всем уважении к профессиональным математикам хотелось бы иметь больше
книг по математике, написанных инженерами и физиками. Несмотря на то,
что физики и инженеры смотрят на математику иначе, чем чистые и
строгие математики, писать об этом они не торопятся. Причина здесь,
по нашему мнению, в том, что в общественном мнении слишком сильно
утвердилось заблуждение об особом статусе математического знания, как
принципиально отличного от всего остального естествознания. Инженер,
понимая, что он использует математику не совсем так, как написано в
ортодоксальных учебниках, скорее склонен скрыть этот постыдный, по
его мнению, факт, чем поделиться своим опытом с другими, и очень
жаль. Не следует слишком серьезно относиться к мифам и заблуждениям,
даже если они освящены многовековой традицией. Возьмем к примеру миф
об особой роли строгости и точности рассуждений в математике.
Нестрогим мы называем рассуждение, которое может привести к неверному
результату. Но рассуждение, которое может привести к неверному
результату, правильнее называть просто ошибочным. Ошибочных
рассуждений следует избегать, и не имеет значения, о чем идет речь: о
математике, физике или о презренном быте.
И. И. Блехман, А. Д. Мышкис и Я. Г. Пановко
написали очень полезную книгу о логике и особенностях приложений
математики [4]. Прикладная математика –
это как раз та математика, которая имеет применение в естествознании.
Другими словами, указанная группа авторов сделала попытку отстоять
правомерность некоторых "физических" и "технических"
подходов в математике, которые традиционно принято считать
нестрогими.
Представление об ущербности таких методов, утвердившееся среди
профессиональных математиков, настолько велико, что И. И. Блехман,
А. Д. Мышкис и Я. Г. Пановко были вынуждены
сделать соответствующие реверансы с целью предупредить нелицеприятную
критику своих коллег. Один из таких реверансов из раздела "От
авторов" мы приводим ниже.
"Отстаивая наличие специфики прикладного математического
мышления и по необходимости заостряя дискуссионные вопросы, мы отдаем
себе отчет в опасности извращения нашей позиции, которое может
привести к замене "террора дедукции" "разгулом
правдоподобия". Ни одна строка этой книги не должна быть
истолкована как оправдание математической безграмотности, приводящей
к грубым ошибкам.
...
Многие коллеги предупреждали нас, что только вполне зрелые
специалисты правильно поймут общую установку книги, а часть читателей
(в особенности молодежь) может воспринять книгу как некую декларацию
математической распущенности и вседозволенности. И все же мы
рассчитываем, что риск такого грубо ошибочного истолкования
относительно невелик и книгу можно адресовать самому широкому кругу
читателей, не сопровождая ее ограничительной надписью "детям до
16 лет читать запрещено".
Может сложиться впечатление, что в правильной математике
заинтересованы только сами математики, а инженеры и физики только и
ждут момента, чтобы эту строгую и чистую математику исказить и
извратить. В действительности инженеры и физики заинтересованы в
хорошей математике не меньше самих математиков, поскольку в их деле
ошибки могут привести к вполне реальным, а не только воображаемым
проблемам. То, что самолеты летают, автомобили ездят, корабли
плавают, а многие дома служат нам довольно долго, служит
доказательством того, что инженеры и физики вполне правильно понимают
математику, которой пользуются.
Миф о низком уровне строгости рассуждений в остальном мире за
пределами математики возник по недоразумению. Многие математики слабо
разбираются в человеческих проблемах, в то же время подавляющее
большинство людей практически не ориентируется в математике. Я думаю,
что можно совершенно строго доказать, что любой здоровый человек
всегда рассуждает совершенно правильно, если не ошибается, а
ошибается он не чаще, чем среднестатистический математик.
|
1 |
Акивис М.А., Гольдберг В.В. Тензорное исчисление. – М.:
Наука, 1972. – 351 с. |
|
2 |
Александрова Н.В. Математические термины. Справочник. – М.:
"Высшая школа", 1978. – 190 с. |
|
3 |
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в
примерах и задачах: Учеб. пособие для втузов. В 3-х т. Т. 1.
Статика и кинематика. – 9-е изд., перераб. – М.:
Наука, 1990. – 672 с. |
|
4 |
Блехман И.И., Мышкис А.Д., Пановко Я.Г. Механика и
прикладная математика: Логика и особенности приложений
математики. – М.: Наука. Главная редакция
физико-математической литературы, 1983. – 328 с. |
|
5 |
Блох В.И. Теория упругости. – Харьков: Издательство
Харьковского государственного университета, 1964. – 483 с. |
|
6 |
Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.
1: Учеб. пособие для вузов. – 6-е изд. – М.: ООО
"Издательство Оникс": "Издательство Мир и
Образование", 2005. – 304 с. |
|
7 |
Димитриенко Ю.И. Тензорное исчисление: Учебное пособие для вузов.
– М.: Высш. шк., 2001. – 575 с. |
|
8 |
Кильчевский Н.А. Курс теоретической механики. т. 1. – М.:
Наука, 1977. – 480 с. |
|
9 |
Киттель Ч., Найт В., Рудерман М. Механика: Учебное руководство:
Пер. с англ./ Под ред. А.И. Шальникова и А.С. Ахматова. –
3-е изд., испр. – М.: Наука. Главная редакция
физико-математической литературы, 1983. – 448 с. |
|
10 |
Клетеник Д.В. Сборник задач по аналитической геометрии: Учебное
пособие для втузов – СПб: "Специальная литература",
1998. – 200 с. |
|
11 |
Кочин Н.Е. Векторное исчисление и начала тензорного исчисления. –
М.: Наука, 1965. – 424 с. |
|
12 |
Лаптев Г.Ф. Элементы векторного исчисления. – М.: Наука,
1975. – 336 с. |
|
13 |
Рашевский П.К. Риманова геометрия и тензорный анализ. – М.:
Наука, 1967. – 664 с. |
|
14 |
Рублев А.Н. Курс линейной алгебры и аналитической геометрии.
Учебник для втузов. М.: Высшая школа, 1972. 424 с. |
|
15 |
Савельев И.В. Курс общей физики. В 5 кн. Кн. 1 Механика: Учеб.
пособие для втузов / И.В. Савельев. – М.: ООО "Издательство
Астрель": ООО "Издательство АСТ", 2002. –
336 с. |
|
16 |
Садаков О.С. Основы тензорного анализа (применительно к теории
упругости). – Челябинск: Из-во Челябинского
политехнического института, 1981. – 92 с. |
|
17 |
Седов Л.И. Механика сплошной среды, т. 1. 1. – М.: Наука,
1983. – 528 с. |
|
18 |
Сокольников И. Тензорный анализ (с приложениями к геометрии и
механике сплошных сред): Пер. с англ. – М.: Наука, 1971. –
376 с. |
|
19 |
Стренг Г. Линейная алгебра и ее применения. – М.: Мир,
1980. – 454 с. |
|
20 |
Схоутен Я.А. Тензорный анализ для физиков. – М.: Наука,
1965. – 456 с. |
|
21 |
Формальная логика. / ред. И.Я. Чупахин, И.Н. Бродский / –
Л.: "Издательство Ленинградского университета", 1977. –
357 с. |
|
22 |
Хорн Р., Джонсон Ч. Матричный анализ: Пер. с англ. –
М.: Мир, 1989. – 655 с. |
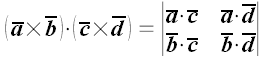 .
.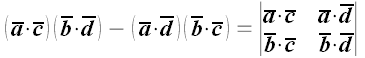
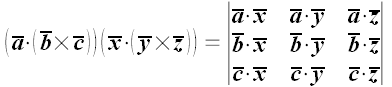
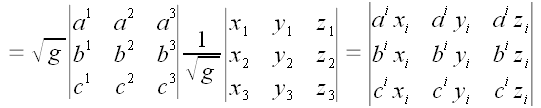
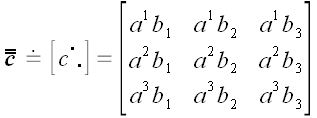 .
.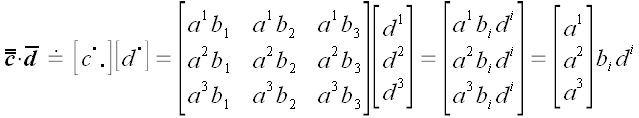 .
.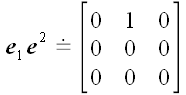 .
.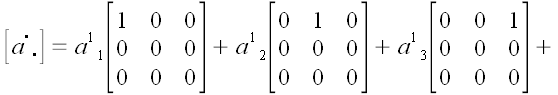
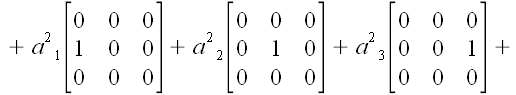
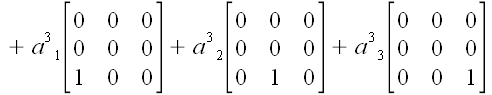 ,
,