Суперобложка / Обложка / Содержание

От автора Введение Векторы .Геометрическое определение вектора .Алгебраические операции над направленными отрезками ..Сложение направленных отрезков ..Умножение направленных отрезков на число .Проекции вектора ..Параллельное проектирование вектора в пространстве ..Параллельное проектирование вектора в пространстве ...Проекция точки на плоскость ...Проекция вектора на плоскость ..Ортогональная проекция вектора в пространстве ...Ортогональная проекция вектора на плоскость ...Ортогональная проекция вектора на прямую и направленную ось .Метод координат ..Коллинеарные векторы ..Компланарные векторы ..Векторы в трехмерном геометрическом пространстве ..Линейная зависимость векторов и размерность пространства .Декартова система координат ..Различные формы записи векторов ..Линейные операции над векторами в координатной форме ..Скалярное умножение векторов ...Свойства скалярного умножения ...Скалярное умножение в декартовых координатах ..Некоторые примеры использования скалярного умножения .Измерение площадей и объемов ..Площадь параллелограмма, построенного на векторах ..Свойства определителя второго порядка ..Задачи на применение определителей ..Объем параллелепипеда, построенного на векторах ..Определитель третьего порядка и его свойства ..Векторное произведение векторов ..Векторное умножение векторов базиса декартовой системы координат На подступах к тензорам .Преобразования координат .Скалярное умножение векторов в произвольных косоугольных координатах .Метрический тензор .Взаимный координатный базис .Ковариантные и контравариантные координаты вектора .Площадь и объем в косоугольных координатах ..Индексная форма записи для выражений с определителями ..Символы Веблена ..Свойства символов Веблена ..Тензор Леви-Чивиты ..Операция векторного умножения в произвольных косоугольных координатах .Линейные преобразования или операторы .Линейный оператор и его матрица ..Примеры линейных операторов .Доказательство теоремы об определителе Тензоры .Определение тензора .Общие определения алгебраических операций с тензорами .Примеры на применение тензоров в физике ..Тензор инерции ..Тензор напряжений .Задачи ..Задачи на тождественные преобразования Методические комментарии Литература

Вернемся к задаче вычисления скалярного произведения в произвольной косоугольной системе координат , и . Мы знаем, что для двух произвольных векторов и

,

и в общем случае ни один из коэффициентов не равен нулю. В развернутом виде выражение достаточно далеко от той идеальной простоты, которую мы имели в декартовой системе координат. Частично положение можно исправить, если для выражения векторов и использовать различные базисы. Действительно, если помимо базиса , , использовать некоторый базис , , (верхнее положение индексов мы использовали для того, чтобы отличить этот базис от основного) и при этом потребовать, чтобы (порядок индексов в символах Кронекера не имеет значения), то

, где означает координату вектора во вспомогательном базисе .

Заручившись поддержкой вспомогательной системы координат, которую принято называть взаимной, мы получаем максимально простое выражение для скалярного умножения.

Сама же взаимная система координат полностью определяется основной системой и условиями , которые словами можно выразить так:

1. Каждый базисный вектор взаимной системы ортогонален ко всем разноименным с ним базисным векторам основной системы.

2. Длина базисного вектора взаимной системы выбирается таким образом, чтобы скалярное произведение его на одноименный вектор основной системы равнялось единице.

Сами векторы взаимного базиса удобнее всего вычислить через их координаты. Координаты можно вычислить либо в основном базисе, либо в некотором вспомогательном. Мы используем обе эти возможности. Для начала покажем, как можно вычислить координаты векторов взаимного базиса во вспомогательной декартовой системе координат. Воспользуемся тем, что

.

Пусть и – координаты векторов основного и взаимного базисов в декартовой системе координат, тогда

.

Умножив правую и левую часть уравнения на матрицу

, получим

, или в краткой записи .

То есть матрица координат взаимного базиса равна обратной и транспонированной матрице координат основного базиса в некоторой декартовой системе координат.

Рассмотрим простой в вычислительном отношении пример на нахождение взаимного базиса для системы координат на плоскости.

Пусть векторы основного базиса и (рис. 45) заданы своими координатами в декартовой системе координат:

и .

Тогда

; ; .

Следовательно,

и .

Нахождение взаимного базиса в пространстве усложняется только за счет процедуры вычисления обратной матрицы, других принципиальных отличий нет.

Теперь воспользуемся другой более общей возможностью и выразим векторы взаимного базиса через векторы основного: . Умножим скалярно данное уравнение на вектор :

.

В свое время для скалярного произведения векторов основного базиса мы ввели обозначение . Логично тот же принцип использовать и для обозначения скалярного произведения векторов взаимного базиса: . Следовательно, .

Теперь равенство умножим слева и справа на вектор : . Из чего можно заключить, что матрица, составленная из коэффициентов , является обратной по отношению к матрице метрического тензора, то есть . Отсюда также следует, что в принятых нами ранее обозначениях. Коэффициенты матриц и принято рассматривать как координаты одного и того же метрического тензора только в разных координатных системах – основной и взаимной.

Вернемся к нахождению векторов взаимного базиса.

Пусть и – векторы основного базиса, причем , угол между ними (рис. 46).

Найдем координаты метрического тензора в основном и во взаимном базисах.

;

.

И, воспользовавшись уравнением , находим векторы взаимного базиса

.

Откуда получаем:

и .

Основная и взаимная системы координат связаны друг с другом соотношениями . Выбирая основную систему, мы автоматически определяем и взаимную систему координат. Мы знаем, что при переходе к новым координатам, векторы базисов новой и старой систем координат связаны соотношением

,

которое принято называть ковариантным преобразованием. Соответственно и векторы основного базиса, и индексы, которыми они пронумерованы, называются ковариантными.

Координаты вектора в основной системе координат изменяются в соответствии с другим законом:

,

который называется контравариантным. Матрица, определяющая контравариантное преобразование, является обратной и транспонированной по отношению к матрице ковариантного преобразования:

.

С этим и связан выбор названий – ковариантный и контравариантный. Соответственно и координаты вектора в основной системе координат, и индексы, которыми они пронумерованы, называются контравариантными. Ковариантные индексы принято писать внизу, а контравариантные – вверху. Мы с самого начала старались придерживаться этого правила, хотя до настоящего момента нам было сложно объяснить причину необычного для индекса верхнего положения.

Мы пока еще не пытались выяснить законы преобразования векторов взаимного базиса и координат векторов в этом базисе, но если принятые нами обозначения не являются случайными, то векторы взаимного базиса должны быть контравариантными, а координаты – ковариантными. Проверим это предположение. Для начала найдем закон преобразования контравариантных координат метрического тензора. Все операции будем выполнять в индексной форме с дословным переводом на язык матриц. Начнем с того, что матрицы и координат метрического тензора являются взаимно обратными, следовательно, и .

;

.

Здесь мы использовали известный закон преобразования ковариантных координат метрического тензора.

;

Умножаем на и суммируем по всем возможным значениям индекса n'. Такая операция называется сверткой по индексу n'. В матричном виде операции свертки соответствует умножение на матрицу .

.

Матрицы и взаимно обратные, поэтому и .

.

При свертке с символом Кронекера общий текущий индекс n в заменяется на второй символ m.

.

Свертываем правую и левую части равенства с .

;

.

Свертываем с .

;

.

В этом выводе мы постарались продемонстрировать некоторые часто используемые приемы работы с индексами. Матричный перевод мы привели только в порядке пояснения, поскольку действия с матрицами более привычны. В данном случае преобразования в индексной форме не очень эффективны, поскольку мы вынуждены несколько раз последовательно выполнять операцию свертки. Выполняя те же преобразования только в матричной форме, мы быстрее приходим к результату. Покажем это на сей раз без комментариев.

;

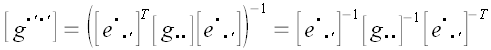
А так как , а , то

, вот и все.

Приведем для сравнения оба закона вместе.

Теперь перейдем к законам преобразования для векторов взаимного базиса и ковариантных координат вектора.

, следовательно .

А что мы можем сказать про ковариантные координаты вектора, то есть про координаты вектора во взаимном базисе? До сих пор мы говорили только про сам базис, и еще ни разу не представилась возможность поговорить о координатах. Начнем с того, что мы знаем, то есть с контравариантных координат.

Пусть произвольный вектор. Воспользуемся тем, что . Следовательно, . Откуда получаем, что . Аналогично можно получить, что . Сведем полученные результаты в таблицу.

Операции, которые мы свели в таблицу, принято называть операциями поднятия и опускания индексов. Часто используют более образное название – "жонглирование индексами". Операции по жонглированию индексами выполняются при помощи метрического тензора и позволяют легко переходить от ковариантных координат к контравариантным, и наоборот.

Перейдем к законам преобразования ковариантных координат вектора при изменении системы координат.

Пусть произвольный вектор, заданный своими ковариантными координатами в старой системе координат. Запишем тот же самый вектор в новой системе координат: . Следовательно, .

Сведем законы преобразования для векторов базиса и координат векторов в одну таблицу.

Приведенная таблица дает полное представление о ковариантных и контравариантных преобразованиях. Только не следует думать, что все это необходимо запомнить. Принятая система обозначений сама напомнит, как правильно записать то или иное преобразование.

Кстати, поскольку в декартовой системе координат , то и . Следовательно, . Другими словами, в декартовой системе координат можно не делать различия между верхними и нижними индексами .