В.
Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Суперобложка /
Обложка /
Содержание

..Параллельное проектирование вектора в пространстве
Проекция точки на плоскость
Проецирование точки на плоскость производится способом аналогичным
проецированию точки на прямую в плоскости. Проекцией
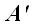 точки A на плоскость α
в направлении вектора
точки A на плоскость α
в направлении вектора
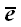 называется точка пересечения плоскости и прямой, проведенной через
эту точку в направлении проецирования (рис. 7, а).
называется точка пересечения плоскости и прямой, проведенной через
эту точку в направлении проецирования (рис. 7, а).
а) 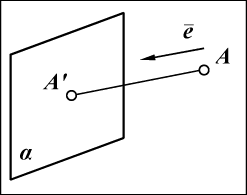 б)
б) 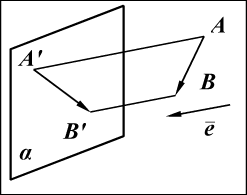 Рис. 7
Рис. 7
Проекция вектора на плоскость
Проекцией вектора
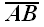 на плоскость α называется вектор
на плоскость α называется вектор
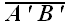 (рис. 7, б), где точки
(рис. 7, б), где точки
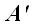 и
и
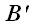 являются проекциями точек
являются проекциями точек
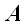 и
и
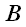 соответственно.
соответственно.
Проекция вектора на прямую
Спроектировать вектор на прямую в пространстве аналогично тому, как
это можно сделать на плоскости, нельзя.
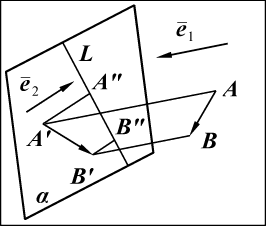 Рис. 8
Рис. 8
Для начала спроектируем вектор
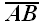 по направлению
по направлению
 на некоторую плоскость, проходящую через прямую L.
На рис. 8 эта плоскость обозначена α. Затем,
полученную таким образом проекцию
на некоторую плоскость, проходящую через прямую L.
На рис. 8 эта плоскость обозначена α. Затем,
полученную таким образом проекцию
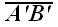 ,
спроектируем по направлению
,
спроектируем по направлению
 (вектор
(вектор
 лежит в плоскости α) на прямую L.
В результате получим вектор
лежит в плоскости α) на прямую L.
В результате получим вектор
 ,
который и принимают за проекцию вектора на прямую. Из построения
очевидно, что проекция вектора не зависит от положения проецируемого
вектора в пространстве. Проще говоря: равные векторы имеют и равные
проекции. Если бы это было не так, мы не имели права говорить о
проекции вектора вообще.
,
который и принимают за проекцию вектора на прямую. Из построения
очевидно, что проекция вектора не зависит от положения проецируемого
вектора в пространстве. Проще говоря: равные векторы имеют и равные
проекции. Если бы это было не так, мы не имели права говорить о
проекции вектора вообще.
Вектор
 (проекция вектора
(проекция вектора
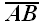 на ось L) можно получить и
более простым способом. В самом деле, точка
на ось L) можно получить и
более простым способом. В самом деле, точка
 является точкой пересечения плоскости, проходящей через точки
является точкой пересечения плоскости, проходящей через точки
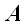 ,
,
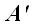 и
и
 и прямой L. Плоскость же,
проходящая через эти точки параллельна векторам
и прямой L. Плоскость же,
проходящая через эти точки параллельна векторам
 и
и
 .
Назовем плоскость параллельную направлениям проецирования
.
Назовем плоскость параллельную направлениям проецирования
 и
и
 проецирующей плоскостью.
проецирующей плоскостью.
Следовательно, можно дать следующее определение проекции вектора на
прямую в пространстве.
Определение (14)
Проекцией вектора
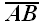 на прямую L по направлению
проецирующей плоскости α называется вектор,
на прямую L по направлению
проецирующей плоскости α называется вектор,
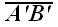 .
Точки
.
Точки
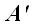 и
и
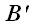 при этом являются точками пересечения прямой L
и плоскостей, проведенных через точки
при этом являются точками пересечения прямой L
и плоскостей, проведенных через точки
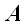 и
и
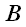 параллельно проецирующей плоскости.
параллельно проецирующей плоскости.
Обозначение
Для обозначения проекции вектора на прямую будем использовать
следующее обозначение:
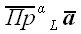 или
или
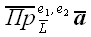 .
.
Проекция вектора на прямую – величина векторная. Совершенно
аналогично тому, что мы имели на плоскости, и для пространственного
случая мы можем ввести понятие алгебраического значения проекции
вектора на направленную ось. Для обозначения алгебраического значения
проекции мы будем (так же как и в "плоском" случае)
использовать то же самое обозначение, только без "векторной"
черты сверху:
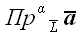 или
или
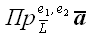 .
И, что очень приятно, теорема (1), которую мы доказали для "плоского"
случая, справедлива и для обеих проекций в пространстве:
.
И, что очень приятно, теорема (1), которую мы доказали для "плоского"
случая, справедлива и для обеих проекций в пространстве:
|
1.
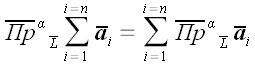 ; ;
|
(1*)
|
|
2.
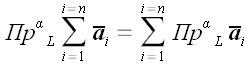 . .
|
(2*)
|
Доказательство полностью аналогично тому, что мы привели для случая
на плоскости.
..Ортогональная проекция вектора в пространстве
Ортогональная проекция есть частный случай параллельной
проекции и, поэтому для нее справедливы те общие результаты, которые
мы уже получили. В то же время ортогональная проекция обладает рядом
геометрических свойств, которые выгодно отличают ее от других видов
проекции. Физика также имеет свой собственный интерес к этому виду
проекции. Например, работа силового поля зависит именно от
ортогональной проекции силы на направление перемещения. Можно,
видимо, утверждать, что ортогональная проекция и, связанная с ней,
ортогональная система координат, о которой мы будем говорить в
дальнейшем, выделена самой природой.
Ортогональная проекция вектора на плоскость
Ортогональную проекцию мы получим, если вектор, задающий направление
проектирования, ортогонален плоскости, на которую производится
проектирование. Поскольку при ортогональном проектировании
направление проектирования задается однозначно самой плоскостью, то в
условном обозначении его можно опустить:
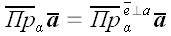 .
.
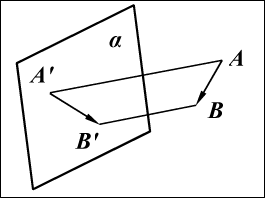 Рис. 9
Рис. 9
Для получения ортогональной проекции вектора на плоскость достаточно
из начала и конца вектора опустить на эту плоскость перпендикуляры.
Основания этих перпендикуляров и определяют проекцию вектора на
плоскость (рис. 9):
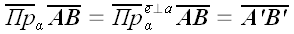 .
.
Ортогональная проекция вектора на прямую и направленную ось
Для построения ортогональной проекции вектора
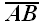 на прямую
на прямую
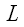 или ось
или ось
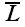 необходимо использовать проектирующую плоскость α
ортогональную прямой, либо просто опустить на прямую
необходимо использовать проектирующую плоскость α
ортогональную прямой, либо просто опустить на прямую
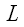 перпендикуляры (
перпендикуляры (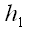 ,
,
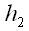 )
из начала и конца вектора
)
из начала и конца вектора
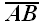 (рис 10).
(рис 10).
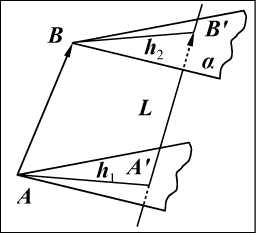 Рис. 10
Рис. 10
В условных обозначениях это запишется так:
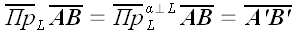 ;
и для алгебраической величины ортогональной проекции вектора на
направленную ось –
;
и для алгебраической величины ортогональной проекции вектора на
направленную ось –
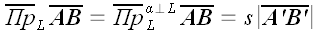 ,
где s – знак плюс или минус.
,
где s – знак плюс или минус.
Теперь придется сказать несколько слов об употреблении термина
"проекция". Мы уже ввели несколько понятий, каждое из
которых претендует на это название: проекция вектора на плоскость,
"векторная" проекция вектора на прямую, алгебраическое
значение проекции вектора на направленную ось, ортогональная проекция
вектора на плоскость, "векторная" ортогональная проекция
вектора на прямую и алгебраическое значение ортогональной проекции
вектора на направленную ось. Наиболее длинным и неудобным по названию
и одновременно наиболее часто используемым является последнее
понятие. В силу этого название "проекция" в векторной
алгебре закрепилось именно за алгебраическим значением ортогональной
проекции вектора на направленную ось. В дальнейшем мы также не будем
отступать от этой традиции, тем более что из контекста обычно всегда
ясно, о чем идет речь.
Итак, проекцией вектора на направленную ось будем называть алгебраическое значение его ортогональной проекции на эту ось.
Мы не будем считать это определением проекции вектора на направленную
ось, а лишь удобным соглашением о названии.
Свойства ортогональной проекции вектора на направленную
ось.
1. Проекция суммы векторов равна сумме их проекций.
Для двух векторов:
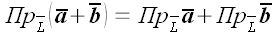 ;
;
и для любого их количества
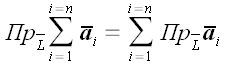 .
.
2. Проекция произведения вектора
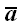 на действительное число λ равна произведению числа λ
на проекцию вектора
на действительное число λ равна произведению числа λ
на проекцию вектора
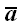 .
.
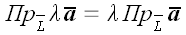 .
.
Если первые два свойства справедливы для всех типов проекций, и мы их
сформулировали более для порядка, то следующее свойство является
"визитной карточкой" ортогональной проекции.
3. Проекция вектора
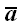 на направленную ось
на направленную ось
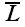 равна произведению его модуля на
равна произведению его модуля на
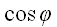 ,
где угол
,
где угол
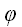 – угол между вектором
– угол между вектором
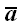 и направленной осью
и направленной осью
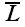 (рис. 11). Дадим этому свойству доказательство.
(рис. 11). Дадим этому свойству доказательство.
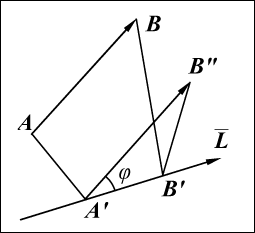 Рис. 11
Рис. 11
Доказательство
Спроектируем точки
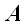 и
и
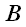 (конечно, ортогонально) на прямую
(конечно, ортогонально) на прямую
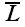 .
Вектор
.
Вектор
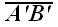 есть проекция вектора
есть проекция вектора
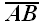 :
:
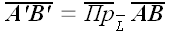 .
Перенесем вектор
.
Перенесем вектор
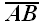 параллельно самому себе так, чтобы точка
параллельно самому себе так, чтобы точка
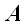 совпала с точкой
совпала с точкой
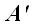 .
Минимальный угол между векторами
.
Минимальный угол между векторами
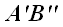 и
и
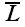 принимается за угол принимается за угол φ между вектором и
осью. Поскольку равные векторы имеют и равные проекции, то проекции
векторов
принимается за угол принимается за угол φ между вектором и
осью. Поскольку равные векторы имеют и равные проекции, то проекции
векторов
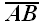 и
и
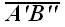 одинаковы и равны
одинаковы и равны
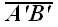 .
Алгебраическая величина проекции вектора
.
Алгебраическая величина проекции вектора
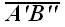 ,
или просто проекция, в соответствии с соглашением о названиях, равна
,
или просто проекция, в соответствии с соглашением о названиях, равна
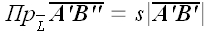 ,
где s означает знак "плюс"
или "минус". А модуль вектора
,
где s означает знак "плюс"
или "минус". А модуль вектора
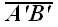 ,
в свою очередь, равен произведению модуля вектора
,
в свою очередь, равен произведению модуля вектора
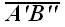 на
на
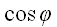 :
:
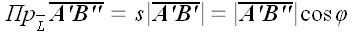 .
.
Учитывая, что
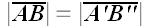 и
и
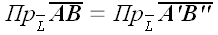 ,
получаем окончательно
,
получаем окончательно
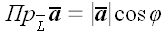 .
.

 б)
б) 

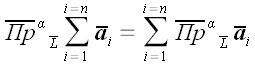 ;
;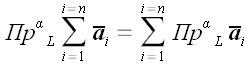 .
.

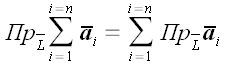 .
.