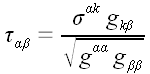В.
Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Суперобложка /
Обложка /
Содержание


Проделанная
нами работа позволяет сделать некоторые обобщения. Последовательно
развивая координатный метод в теории векторов, мы постоянно
оказываемся перед необходимостью работать с различными массивами
чисел. Наиболее простой из них – это массив координат вектора.
Затем необходимость выразить метрические отношения геометрического
пространства приводит нас к массиву координат метрического тензора.
Это уже двухмерный массив, обладающий более сложным строением.
Потребность выразить функциональные отношения между векторами
приводит к понятию линейного оператора, координаты которого также
образуют двухмерный массив. Еще раньше понятие ориентированного
объема приводит нас к трехмерному массиву координат тензора
Леви-Чивиты.
Представим теперь, что нам понадобилось выразить линейную
функциональную зависимость между двумя операторами
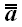 и
и
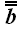 .
Понятно, что нам для этого потребуется массив чисел с четырьмя
индексами:
.
Понятно, что нам для этого потребуется массив чисел с четырьмя
индексами:
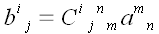 .
Открыв таким образом двери перед векторными величинами, мы не можем
уже отказаться от применения массивов с произвольным количеством
индексов.
.
Открыв таким образом двери перед векторными величинами, мы не можем
уже отказаться от применения массивов с произвольным количеством
индексов.
Следующее важное наблюдение, которое можно сделать, заключается в
том, что
массивы,
о
которых
идет
речь,
существуют
не
сами
по
себе,
а
всегда
связаны
с
некоторой
системой
координат
. Можно сказать, что они
всегда заданы в определенной системе координат и изменяются по
известному закону при переходе к другой системе. Закон преобразования
координат массивов копирует закон преобразования координат
ковариантных и контравариантных координат векторов.
Над массивами можно выполнять алгебраические операции как над едиными
объектами, получая при этом объекты того же типа, то есть новые
массивы с теми же самыми законами преобразования координат. Это
положение может показаться спорным, если учесть, что скалярное
умножение двух векторов равно числу. Число не есть массив, и оно не
изменяется при изменении координатной системы. Однако это исключение
легко обойти, если положить, что число – это массив нулевой
размерности, то есть с нулевым количеством индексов.
Общий закон изменения координат массивов с законом изменения
координат векторов позволяет строить математические выражения не
зависимые от случайного выбора координатных систем.
Все это является основанием для того, чтобы выделить такие массивы
как особый предмет для самостоятельного изучения. Для этого нам
необходимо только дать им особое название и соответствующее
определение. Все это было уже сделано итальянскими математиками Риччи
и Леви-Чивитой в 1901 г. Новый математический объект получил название
тензора, а наука о тензорах была названа тензорным исчислением.
Общее определение тензора (29)
Тензором размерности p + q мы будем называть массив
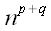 чисел
чисел
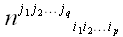 ,
заданных в каждой координатной системе и занумерованных p
индексами внизу и q индексами
наверху, преобразующихся при переходе от одной координатной системы к
другой по закону:
,
заданных в каждой координатной системе и занумерованных p
индексами внизу и q индексами
наверху, преобразующихся при переходе от одной координатной системы к
другой по закону:
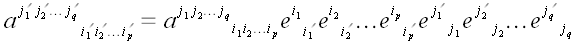 .
.
Числа
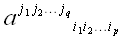 мы будем называть координатами тензора в соответствующей координатной
системе. Все индексы пробегают значения 1, 2, 3 ..., n
независимо друг от друга.
мы будем называть координатами тензора в соответствующей координатной
системе. Все индексы пробегают значения 1, 2, 3 ..., n
независимо друг от друга.
Наиболее общей интерпретацией тензора является линейный оператор.
Коэффициенты линейного оператора в любой координатной системе
являются координатами тензора. Привычный геометрический вектор также
может быть интерпретирован как линейный оператор. Однако с конкретным
тензором может быть связан не один, а несколько линейных операторов,
поэтому, понятия линейного оператора и тензора, хотя и близки, не
являются тождественными.
Алгебраические
операции с тензорами вводятся таким образом, чтобы в результате их
применения мы всегда снова получали бы тензоры. Для того чтобы это
проверить, достаточно проконтролировать закон изменения координат.
Сложение тензоров
Складывать можно только тензоры одинакового строения, например,
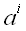 и
и
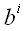 ;
;
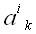 и
и
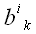 .
Сложение тензоров заключается в почленном сложении элементов обоих
массивов с одинаковыми номерами. В результате сложения образуется
новый массив или тензор того же строения:
.
Сложение тензоров заключается в почленном сложении элементов обоих
массивов с одинаковыми номерами. В результате сложения образуется
новый массив или тензор того же строения:
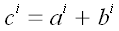 ;
;
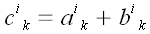 .
.
Умножение тензоров
Умножать можно любые тензоры друг на друга. При умножении каждая
координата одного тензора умножается на каждую координату другого.
Пусть, к примеру, мы перемножаем два тензора
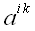 и
и
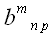 ,
тогда в результате мы получим новый тензор
,
тогда в результате мы получим новый тензор
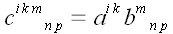 .
С этой операцией мы сталкивались при умножении тензоров Леви-Чивиты.
При перемножении
.
С этой операцией мы сталкивались при умножении тензоров Леви-Чивиты.
При перемножении
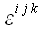 и
и
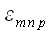 мы получаем шестимерный массив координат, каждый элемент которого
вычисляется как обобщенный символ Кронекера:
мы получаем шестимерный массив координат, каждый элемент которого
вычисляется как обобщенный символ Кронекера:
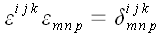 .
.
При умножении тензоров размерность все время увеличивается. От этой
операции не было бы большой пользы, если бы не было другой операции,
которая может размерность понижать.
Свертывание тензора, свертывание тензоров
Свертывание тензора заключается в сложении всех элементов массива с
одинаковыми значениями одного верхнего и одного нижнего индексов при
фиксированных значениях остальных:
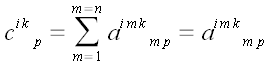 .
.
В этом случае говорят, что мы свернули тензор по второму и четвертому
индексам. Полученный в результате свертки тензор
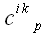 зависит только от остальных индексов, не участвующих в операции. С
операцией свертывания мы встречались при скалярном умножении
векторов:
зависит только от остальных индексов, не участвующих в операции. С
операцией свертывания мы встречались при скалярном умножении
векторов:
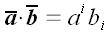 .
Операцию свертывания иногда удобно записывать при помощи символа
Кронекера:
.
Операцию свертывания иногда удобно записывать при помощи символа
Кронекера:
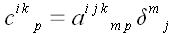 .
.
Мы знаем, что произведению двух линейных операторов
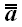 и
и
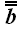 соответствует линейный оператор
соответствует линейный оператор
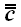 ,
матрица координат которого равна произведению матриц координат
операторов
,
матрица координат которого равна произведению матриц координат
операторов
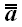 и
и
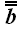 :
:
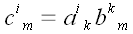 .
Операция умножения тензоров определена таким образом, что она не
соответствует операции умножения операторов. Для того, чтобы найти
тензор, соответствующий произведению операторов, мы должны выполнить
две операции над тензорами. Сначала необходимо тензоры перемножить:
.
Операция умножения тензоров определена таким образом, что она не
соответствует операции умножения операторов. Для того, чтобы найти
тензор, соответствующий произведению операторов, мы должны выполнить
две операции над тензорами. Сначала необходимо тензоры перемножить:
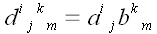 .
Затем свернуть по паре индексов:
.
Затем свернуть по паре индексов:
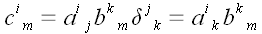 .
Такую операцию, которая заключается в умножении двух тензоров с
последующим свертыванием по индексам, один из которых принадлежит
одному тензору, а второй другому, называется операцией свертывания
тензоров. Тензоры можно свертывать по любому количеству индексов,
например:
.
Такую операцию, которая заключается в умножении двух тензоров с
последующим свертыванием по индексам, один из которых принадлежит
одному тензору, а второй другому, называется операцией свертывания
тензоров. Тензоры можно свертывать по любому количеству индексов,
например:
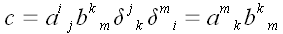 ,
в результате получаем скаляр.
,
в результате получаем скаляр.
Перестановка индексов (транспонирование)
Эта операция нам также уже встречалась. Для тензоров с двумя
индексами данная операция называется транспонированием, а тензор,
который получается в результате применения данной операции,
называется транспонированным тензором. Пусть, например, тензор
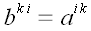 ,
то есть элементы тензора
,
то есть элементы тензора
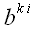 равны элементам
равны элементам
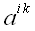 другого тензора. Тензор
другого тензора. Тензор
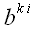 в этом случае называется транспонированным тензором и обозначается
в этом случае называется транспонированным тензором и обозначается
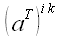 ,
то есть:
,
то есть:
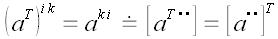 .
Транспонированному тензору размерности два соответствует
транспонированная матрица. Если индексы имеют различный тип, то это
также требуется учесть при перестановке:
.
Транспонированному тензору размерности два соответствует
транспонированная матрица. Если индексы имеют различный тип, то это
также требуется учесть при перестановке:
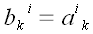 .
.
Использование метрического тензора позволяет, как мы уже знаем,
задать еще одну тензорную операцию.
Операция поднятия и опускания индексов тензора
Например,
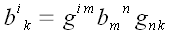 .
Следовательно, если
.
Следовательно, если
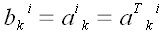 (предыдущий пример), то
(предыдущий пример), то
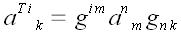 или в матричной форме:
или в матричной форме:
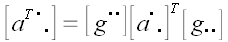 .
.
Операция транспонирования тензора по индексам различного типа
является более сложной операцией, чем может показаться на первый
взгляд и об этом не следует забывать.
Теперь, когда мы дали общее определение тензора и операций над
тензорами, мы видим, что все это нам уже знакомо. Так или иначе, и с
тензорами и с операциями над ними мы уже сталкивались, только мы не
знали, с чем имеем дело. Конечно это не вся теория, это только ее
начало, но, тем не менее, все то, что хотелось бы сказать об этом
предмете в книге для начинающих, мы уже сказали.
..Тензор инерции
Вычислим момент импульса
 вращающегося твердого тела относительно некоторой оси, проходящей
через начало координат, с угловой скоростью
вращающегося твердого тела относительно некоторой оси, проходящей
через начало координат, с угловой скоростью
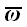 .
Разобьем тело на материальные точки объемом dV и массой dm.
Запишем момент импульса для одной материальной точки.
.
Разобьем тело на материальные точки объемом dV и массой dm.
Запишем момент импульса для одной материальной точки.
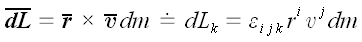 ;
;
Скорость точек при вращательном движении определяется как векторное
произведение угловой скорости на радиус вектор точки.
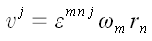 ;
;
Следовательно:
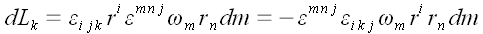 ;
;
Свернем тензоры Леви-Чивиты.
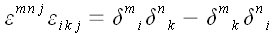 ;
;
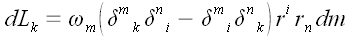 ;
;
Просуммировав моменты импульсов всех материальных точек по всему
объему тела, найдем момент импульса для тела в целом.
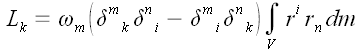 ;
;
Введем обозначение:
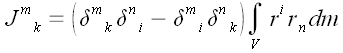 ;
;
И с учетом обозначения:
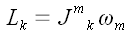 ;
;
Массив из девяти чисел
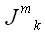 называется тензором инерции. Тензор инерции выражает зависимость
между угловой скоростью и моментом импульса тела. Его координаты
определяются распределением масс тела относительно оси вращения.
называется тензором инерции. Тензор инерции выражает зависимость
между угловой скоростью и моментом импульса тела. Его координаты
определяются распределением масс тела относительно оси вращения.
Используя свойства метрического тензора, получаем связь для
контравариантных координат векторов
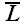 и
и
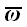 .
.
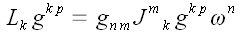 ;
;
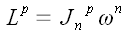 .
.
Наиболее простые выражения для координат тензора момента инерции мы
получаем в декартовой системе координат.
Осевые моменты инерции
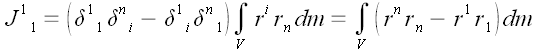 ;
;
В декартовой системе
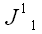 обозначается –
обозначается –
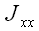 называется осевым моментом инерции.
называется осевым моментом инерции.
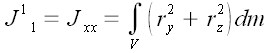 ;
;
Далее аналогично:
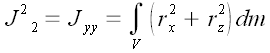 ;
;
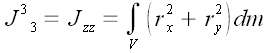 ;
;
Центробежные моменты инерции
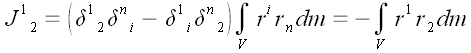 ;
;
В декартовой системе координат
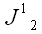 обозначается
обозначается
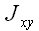 и называется центробежным моментом инерции.
и называется центробежным моментом инерции.
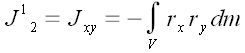 ;
;
Далее аналогично:
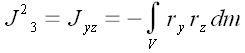 ;
;
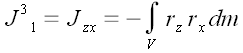 ;
;
В матричной форме:
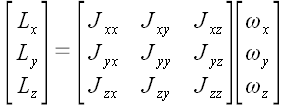 .
.
Теперь вычислим кинетическую энергию вращающегося тела. Воспользуемся
тем же приемом: разобьем тело на материальные точки и вычислим
сначала энергию для одной точки. Дальнейшие преобразования понятны
без комментариев.
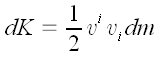 ;
;
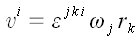 ;
;
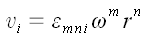 ;
;
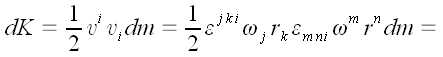
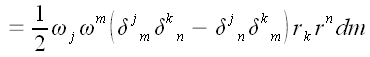 .
.
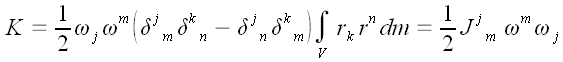
В матричной форме:
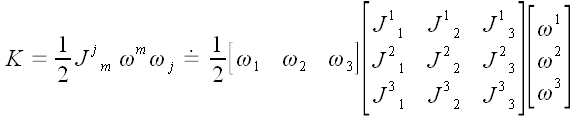 .
.
..Тензор
напряжений
Пусть упругое твердое тело находится в равновесии под действием
внешних и внутренних сил. Мысленно вырежем из этого тела элемент в
форме параллелепипеда (рис. 52).
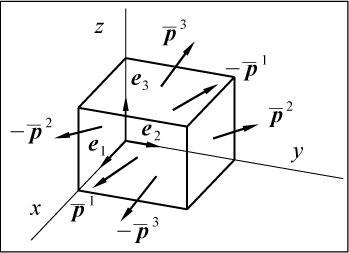 Рис. 52
Рис. 52
Если размеры элемента достаточно малы, то можно считать, что
напряжения, действующие в его гранях, постоянны в пределах каждой
грани. Кроме того, напряжения на противоположных гранях равны по
величине и противоположны по направлению. Напряжения обозначены
символом
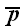 с индексом, который указывает номер вектора базиса, совпадающего с
нормалью к соответствующей грани. Например,
с индексом, который указывает номер вектора базиса, совпадающего с
нормалью к соответствующей грани. Например,
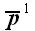 – напряжение, которое действует в грани параллелепипеда
нормальной к вектору базиса
– напряжение, которое действует в грани параллелепипеда
нормальной к вектору базиса
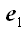 ,
на рис. 52 это передняя грань
параллелепипеда. В противоположной грани, следовательно, действует
напряжение
,
на рис. 52 это передняя грань
параллелепипеда. В противоположной грани, следовательно, действует
напряжение
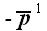 .
Отсечем от параллелепипеда тетраэдр, как показано на рис. 53.
.
Отсечем от параллелепипеда тетраэдр, как показано на рис. 53.
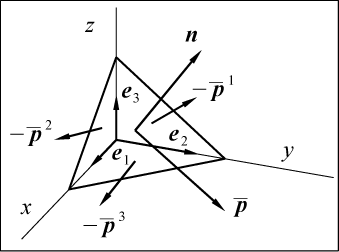 Рис. 53
Рис. 53
Три грани получившегося тетраэдра совпадают с координатными
плоскостями, положение четвертой грани задается вектором нормали n.
Напряжение, которое действует в четвертой грани неизвестно и мы
обозначили его через
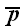 .
Если изменять положение этой плоскости и соответственно и вектора
нормали n, то мы будем
получать различные значения напряжения
.
Если изменять положение этой плоскости и соответственно и вектора
нормали n, то мы будем
получать различные значения напряжения
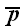 .
Вектор
.
Вектор
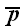 ,
следовательно, является векторной функцией вектора нормали n:
,
следовательно, является векторной функцией вектора нормали n:
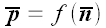 .
Для того чтобы найти эту функцию, рассмотрим равновесие тетраэдра.
Площади граней тетраэдра, в которых действуют напряжения
.
Для того чтобы найти эту функцию, рассмотрим равновесие тетраэдра.
Площади граней тетраэдра, в которых действуют напряжения
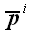 ,
мы обозначим соответственно
,
мы обозначим соответственно
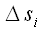 .
Площадь четвертой грани обозначим
.
Площадь четвертой грани обозначим
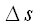 .
Поскольку тетраэдр находится в равновесии, то сумма всех сил,
действующих на него, должна равняться нулю:
.
Поскольку тетраэдр находится в равновесии, то сумма всех сил,
действующих на него, должна равняться нулю:
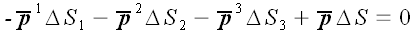 ;
;
Поделив уравнение на
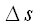 и, используя то, что
и, используя то, что
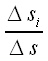 равно косинусу угла наклона единичной нормали n
к координатным осям, получим:
равно косинусу угла наклона единичной нормали n
к координатным осям, получим:
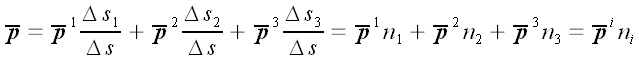 .
.
Разложим каждый из векторов напряжений по векторам базиса:
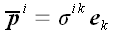 .
.
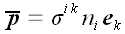 ,
и в координатной форме
,
и в координатной форме
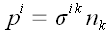 .
.
Мы получили формулу, позволяющую по положению нормали к плоскости
вычислить действующее в этой плоскости напряжение. Коэффициенты
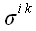 образуют тензор, который называется тензором напряжения. В декартовой
системе координат координаты тензора напряжения имеют простой
физический смысл: они равны нормальным и касательным напряжениям в
соответствующих координатных площадках.
образуют тензор, который называется тензором напряжения. В декартовой
системе координат координаты тензора напряжения имеют простой
физический смысл: они равны нормальным и касательным напряжениям в
соответствующих координатных площадках.
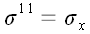 ;
;
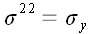 ;
;
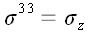 ;
;
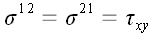 ;
;
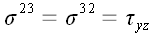 ;
;
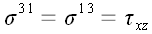 .
.
Нормальное напряжение в произвольной площадке мы можем найти как
проекцию вектора напряжения
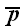 на направление нормали n.
на направление нормали n.
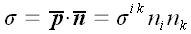 .
.
Для того, чтобы найти касательное напряжение в плоскости, необходимо
задать направление при помощи единичного вектора
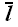 ,
лежащего в этой плоскости. В этом случае касательное напряжение в
плоскости с нормалью n в
направлении вектора
,
лежащего в этой плоскости. В этом случае касательное напряжение в
плоскости с нормалью n в
направлении вектора
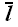 может быть вычислено по формуле:
может быть вычислено по формуле:
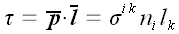 .
.
До сих пор мы пользовались декартовой координатной системой, но ничто
нам не мешает, пользуясь известными правилами, перейти к произвольной
системе координат. Выразим векторы
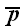 и n через их координаты в
новой координатной системе.
и n через их координаты в
новой координатной системе.
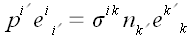 ;
;
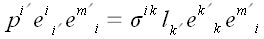 ;
;
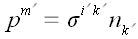 ,
где
,
где
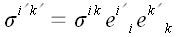 .
.
Из этих преобразований следует, что
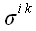 преобразуется вполне по тензорному закону, что оправдывает его
название. К сожалению, ясный физический смысл координат тензора
преобразуется вполне по тензорному закону, что оправдывает его
название. К сожалению, ясный физический смысл координат тензора
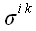 в произвольной координатой системе не сохраняется.
в произвольной координатой системе не сохраняется.
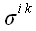 больше не совпадают с нормальными и касательными напряжениями на
соответствующих площадках. Но, несмотря на это,
больше не совпадают с нормальными и касательными напряжениями на
соответствующих площадках. Но, несмотря на это,
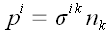 являются координатами вектора напряжения в любой координатной
системе. И мы можем воспользоваться этими уравнениями для того, чтобы
найти физические напряжения на координатных площадках косоугольной
системы координат. Вычислим напряжение на площадке, образованной
базисными векторами
являются координатами вектора напряжения в любой координатной
системе. И мы можем воспользоваться этими уравнениями для того, чтобы
найти физические напряжения на координатных площадках косоугольной
системы координат. Вычислим напряжение на площадке, образованной
базисными векторами
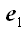 и
и
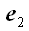 .
В качестве нормали используем вектор
.
В качестве нормали используем вектор
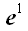 ,
который к ним ортогонален.
,
который к ним ортогонален.
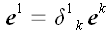 ;
;
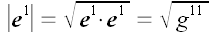 .
.
Единичный вектор нормали равен
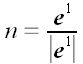 .
.
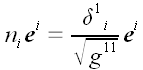 ;
;
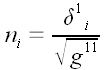 .
.
Теперь находим напряжение на площадке.
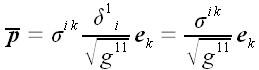 .
.
Находим проекцию вектора
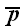 на вектор n, которая и
является нормальным напряжением на этой площадке.
на вектор n, которая и
является нормальным напряжением на этой площадке.
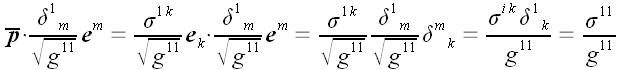 .
.
Аналогичные выражения можно получить и для других координатных
площадок. Обозначив напряжение на координатной площадке с вектором
нормали
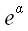 символом
символом
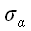 ,
мы можем записать одно общее уравнение для всех трех площадок:
,
мы можем записать одно общее уравнение для всех трех площадок:
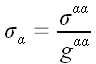 .
Здесь и далее суммирование по греческим символам не производится.
.
Здесь и далее суммирование по греческим символам не производится.
Мы также можем найти касательные напряжения в координатных площадках
в направлении координатных осей, как ортогональные проекции
соответствующих векторов напряжений на направления осей.
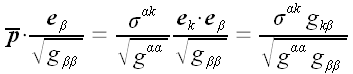 ,
где
,
где
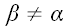 .
.
Обозначив касательное напряжение в координатной площадке с вектором
нормали
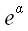 в направлении координатной оси
в направлении координатной оси
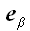 (
(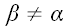 )
символом
)
символом
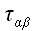 ,
мы можем записать одно общее уравнение для всех шести возможных
вариантов:
,
мы можем записать одно общее уравнение для всех шести возможных
вариантов:
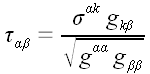
Из полученных выражений следует, что реальные физические напряжения
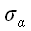 и
и
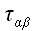 в координатных площадках косоугольной системы координат не равны
координатам тензора напряжения
в координатных площадках косоугольной системы координат не равны
координатам тензора напряжения
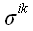 и сами не образуют тензора.
и сами не образуют тензора.
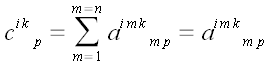 .
.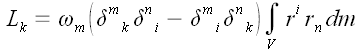 ;
;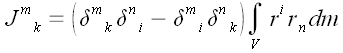 ;
;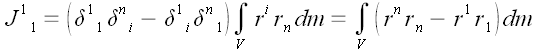 ;
;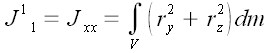 ;
; ;
;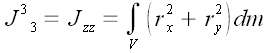 ;
;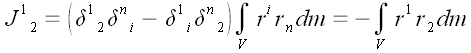 ;
;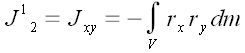 ;
;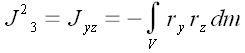 ;
;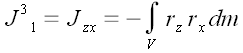 ;
;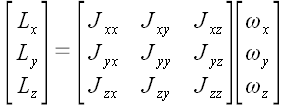 .
.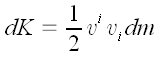 ;
;
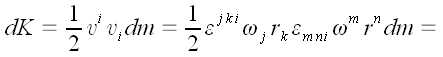
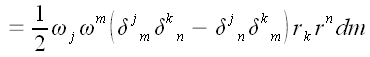 .
.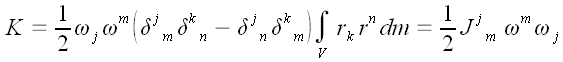
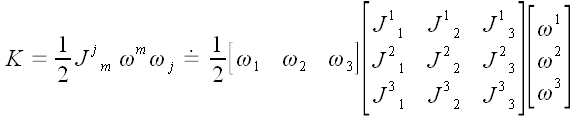 .
.

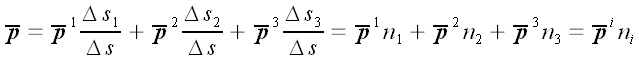 .
.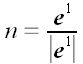 .
.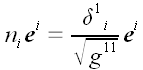 ;
;
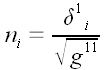 .
.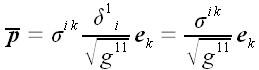 .
.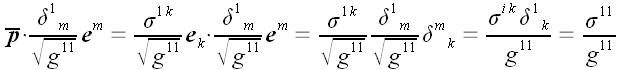 .
.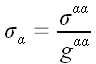 .
Здесь и далее суммирование по греческим символам не производится.
.
Здесь и далее суммирование по греческим символам не производится.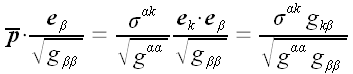 ,
где
,
где