В.
Г. Автор. Векторная и тензорная алгебра для будущих физиков и
техников
Суперобложка /
Обложка /
Содержание

..Примеры линейных операторов
1. Оператор тождественного преобразования.
Оператор тождественного преобразования переводит любой вектор сам в
себя. Другими словами, он возвращает тот же самый вектор, который
принял, ничего с ним не делая. Оператор тождественного преобразования
обозначается буквой I,
следовательно:
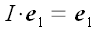 ,
,
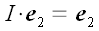 и
и
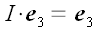 .
Отсюда находим матрицу тождественного преобразования.
.
Отсюда находим матрицу тождественного преобразования.
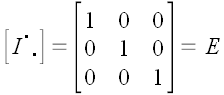 .
.
Проверим закон преобразования координат тождественного преобразования
при смене координатной системы.
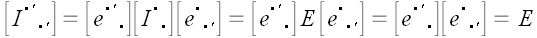 .
.
Следовательно, как, впрочем, и можно было ожидать, матрица оператора
тождественного преобразования равна единичной матрице.
Умножим матрицу тождественного преобразования на матрицу координат
метрического тензора.
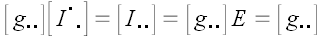 ,
следовательно,
,
следовательно,
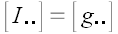 .
.
Аналогично можно показать, что
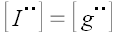 и
и
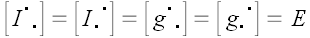 .
.
Отсюда можно сделать вывод, что матрицы тождественного преобразования
и метрического тензора совпадают. Этот факт имеет простое
геометрическое объяснение. Матрица метрического тензора является
матрицей перехода от основной системы координат к взаимной и
наоборот, но вектор, координаты которого преобразуются, остается при
этом тем же самым вектором. Следует заметить, что запись координат
метрического тензора со смешанными индексами, хотя и не запрещена
правилами, обычно не используется. Поскольку
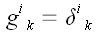 ,
то вместо
,
то вместо
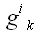 предпочитают записывать
предпочитают записывать
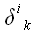 .
Однако при этом не следует забывать, что для символа Кронекера
операции поднятия и опускания индексов не имеют смысла, поэтому
.
Однако при этом не следует забывать, что для символа Кронекера
операции поднятия и опускания индексов не имеют смысла, поэтому
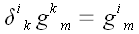 и
и
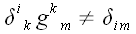 .
.
Матрицу
 некоторые авторы [22] также рассматривают
как матрицу тождественного преобразования особого вида, которое
координаты произвольного вектора в одной координатной системе
преобразует в координаты того же самого вектора, но в новой системе
координат. В этом случае мы не можем говорить о координатах
преобразования в какой-то конкретной системе, так как они зависят от
двух систем координат сразу. Тем не менее мы можем применить
формально общий закон преобразования координат к матрице
некоторые авторы [22] также рассматривают
как матрицу тождественного преобразования особого вида, которое
координаты произвольного вектора в одной координатной системе
преобразует в координаты того же самого вектора, но в новой системе
координат. В этом случае мы не можем говорить о координатах
преобразования в какой-то конкретной системе, так как они зависят от
двух систем координат сразу. Тем не менее мы можем применить
формально общий закон преобразования координат к матрице
 и получим при этом обратную матрицу
и получим при этом обратную матрицу
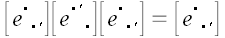 .
.
Мы видим, что матрица тождественного преобразования многолика, и
может принимать вид любой невырожденной матрицы в зависимости от
способа ее трактовки.
Произвольное линейное преобразование также может быть представлено
координатами сразу в двух координатных системах. В самом деле, пусть
 матрица линейного преобразования, которое вектор с координатами
матрица линейного преобразования, которое вектор с координатами
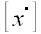 в некоторой системе преобразует в вектор с координатами
в некоторой системе преобразует в вектор с координатами
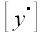 в той же самой системе координат.
в той же самой системе координат.
Тогда
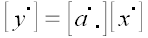 .
.
Выразим координаты вектора
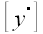 через координаты в новой системе координат.
через координаты в новой системе координат.
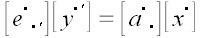 .
.
Умножим правую и левую части равенства на матрицу
 .
.
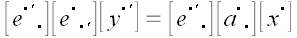 .
.
Учитывая, что
 ,
получим
,
получим
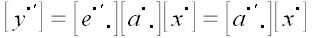 ,
где
,
где
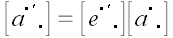 – матрица линейного преобразования, которая координаты вектора
– матрица линейного преобразования, которая координаты вектора
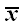 ,
заданные в одной системе, преобразует в координаты вектора
,
заданные в одной системе, преобразует в координаты вектора
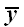 ,
заданные в другой системе координат.
,
заданные в другой системе координат.
Ничего принципиально нового такая возможность не дает, и в дальнейшем
мы не будем рассматривать линейные операторы, отнесенные к двум
системам координат одновременно.
2. Обратный оператор
Если
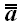 – произвольный оператор, и если существует такой оператор
– произвольный оператор, и если существует такой оператор
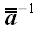 ,
что
,
что
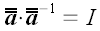 ,
то
,
то
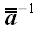 называется обратным оператором. Обратный оператор имеет обратную
матрицу:
называется обратным оператором. Обратный оператор имеет обратную
матрицу:
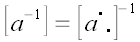 .
Не каждый оператор имеет обратный, а только тот, который осуществляет
взаимно однозначное преобразование.
.
Не каждый оператор имеет обратный, а только тот, который осуществляет
взаимно однозначное преобразование.
3. Оператор растяжения
Представим, что геометрическое пространство построено из эластичного
материала. Растянем его в направлении оси x
так, чтобы каждый отрезок, расположенный вдоль этой оси растянулся бы
в λ раз. В этом случае x
координата каждого вектора увеличится в λ раз, в то же
время остальные его координаты останутся без изменения.
 ;
;
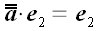 ;
;
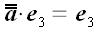 .
.
Мы не вводим специального обозначения для этого оператора.
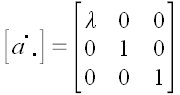 .
.
Теперь, если мы растянем наше пространство по направлениям всех трех
осей, то получим оператор трехосного растяжения:
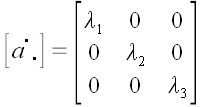 ,
где
,
где
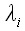 – коэффициенты растяжения вдоль соответствующих осей.
– коэффициенты растяжения вдоль соответствующих осей.
4. Оператор сдвига
Представим, что все пространство заполнено тонкими листами бумаги,
аккуратно сложенными в одну стопку (рис. 50).
Сдвинем листы на одну и ту же величину относительно друг друга в
направлении оси y.
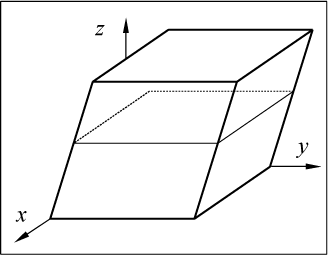 Рис. 50
Рис. 50
Если считать лисы бумаги очень тонкими слоями геометрического
пространства, то векторы, находящиеся в этом пространстве и с ним
связанные также сдвинутся. Координаты векторов параллельных плоскости
xoy, как лежащие в сдвигаемых слоях,
не изменятся. Зато концы вектора перпендикулярного плоскости xoy
сдвинутся один относительно другого в направлении оси y
на величину пропорциональную длине вектора. Общее выражение для
такого преобразования в векторной форме можно записать так:
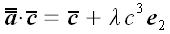 .
Воздействие этого преобразования на векторы базиса можно записать
следующим образом:
.
Воздействие этого преобразования на векторы базиса можно записать
следующим образом:
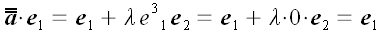 ;
;
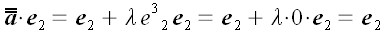 ;
;
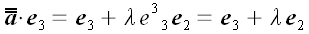 .
.
Отсюда получаем матрицу линейного преобразования сдвига:
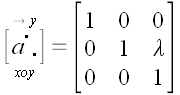 .
.
Аналогично получаем матрицу оператора сдвига в направлении оси y
параллельно плоскости yoz.
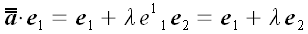 ;
;
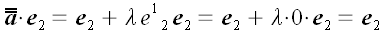 ;
;
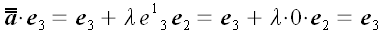 .
.
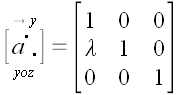 .
.
Матрицы сдвигов относительно других осей получаются точно так же.
5. Оператор поворота относительно координатной оси
Если в предыдущих случаях для вычисления матриц операторов мы могли
использовать произвольную систему координат, то для вычисления
матрицы оператора поворота без декартовой системы координат обойтись
очень трудно. Пусть
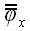 является оператором поворота относительно оси x
декартовой системы координат xyz,
причем поворот осуществляется по направлению от оси y
к z оси. Найдем координаты векторов
базиса, подвергнутых действию этого оператора, на рис. 51 они
обозначены
является оператором поворота относительно оси x
декартовой системы координат xyz,
причем поворот осуществляется по направлению от оси y
к z оси. Найдем координаты векторов
базиса, подвергнутых действию этого оператора, на рис. 51 они
обозначены
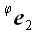 и
и
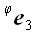 .
.
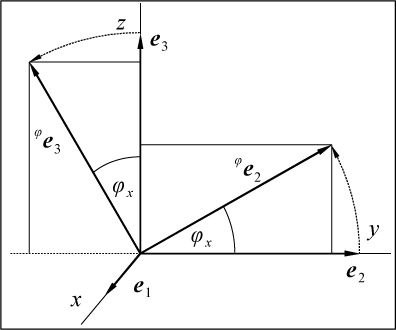 Рис. 51
Рис. 51
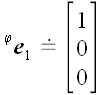 ,
,
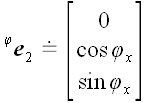 ,
,
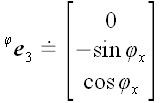 .
.
И, следовательно,
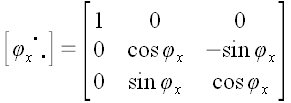
Аналогично можно доказать, что
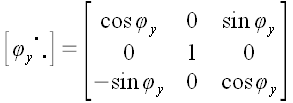 ,
,
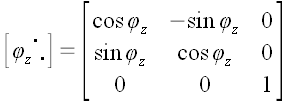 .
.
6. Оператор поворота относительно произвольной оси
Если нам необходимо выполнить преобразование поворота относительно
произвольной оси, не совпадающей ни с одной из координатных осей, мы
можем воспользоваться услугами вспомогательной координатной системы
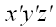 .
Если ось
.
Если ось
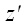 вспомогательной системы координат направить вдоль оси поворота, то
матрица оператора поворота в этой системе запишется уже известным
образом:
вспомогательной системы координат направить вдоль оси поворота, то
матрица оператора поворота в этой системе запишется уже известным
образом:
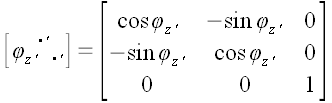 .
.
Теперь достаточно воспользоваться известным законом преобразования
координат оператора, чтобы найти матрицу его координат в старой
системе:
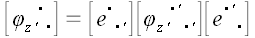 .
Общее выражение для матрицы поворота не отличается ни простотой, ни
красотой и мы ее здесь не приводим, но и не проводя никаких
вычислений, можно сделать некоторые выводы относительно ее свойств.
Умножим матрицу
.
Общее выражение для матрицы поворота не отличается ни простотой, ни
красотой и мы ее здесь не приводим, но и не проводя никаких
вычислений, можно сделать некоторые выводы относительно ее свойств.
Умножим матрицу
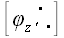 на
на
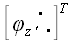 .
.
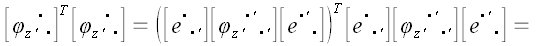
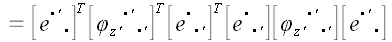 .
.
Матрица преобразования
 составлена из координат векторов базиса системы
составлена из координат векторов базиса системы
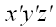 в старой системе координат и, поэтому,
в старой системе координат и, поэтому,
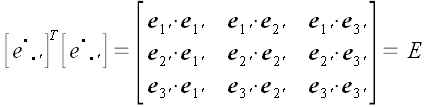 так как система координат является ортонормированной.
так как система координат является ортонормированной.
По аналогичным причинам
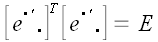 .
То, что
.
То, что
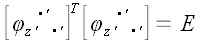 ,
можно проверить непосредственно. Следовательно,
,
можно проверить непосредственно. Следовательно,
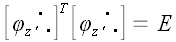 ,
а это означает, что матрица транспонированная к
,
а это означает, что матрица транспонированная к
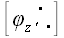 ,
является к ней обратной:
,
является к ней обратной:
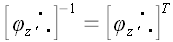 .
Матрицы, обладающие таким свойством и соответствующие им операторы,
называются ортогональными. Следовательно, матрица оператора поворота,
является ортогональной матрицей. Этот факт имеет простое
геометрическое объяснение: как бы мы ни поворачивали первоначально
ортонормированные векторы базиса, они всегда останутся
ортонормированными и, поэтому естественно, что
.
Матрицы, обладающие таким свойством и соответствующие им операторы,
называются ортогональными. Следовательно, матрица оператора поворота,
является ортогональной матрицей. Этот факт имеет простое
геометрическое объяснение: как бы мы ни поворачивали первоначально
ортонормированные векторы базиса, они всегда останутся
ортонормированными и, поэтому естественно, что
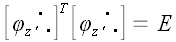 .
Однако, все, что мы до сих пор сказали про оператор поворота,
справедливо только для ортонормированных систем.
.
Однако, все, что мы до сих пор сказали про оператор поворота,
справедливо только для ортонормированных систем.
Пусть теперь
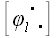 будет оператор поворота в произвольных косоугольных координатах.
Перейдем к ортонормированному базису:
будет оператор поворота в произвольных косоугольных координатах.
Перейдем к ортонормированному базису:
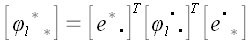 .
.
В ортонормированном базисе
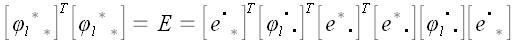 ;
;
Так как
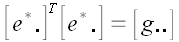 ,
то
,
то
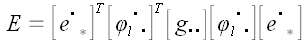 .
.
Умножим правую и левую части равенства на матрицу
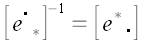 справа и на
справа и на
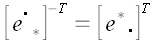 слева.
слева.
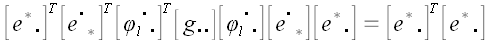 и упрощая далее, получаем
и упрощая далее, получаем
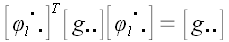 .
Умножая справа на
.
Умножая справа на
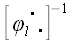 и слева на
и слева на
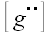 ,
получим:
,
получим:
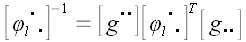 .
.
Вообще для произвольного оператора
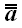 ,
оператором, сопряженным к нему
,
оператором, сопряженным к нему
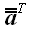 ,
называется оператор, матрица которого равна
,
называется оператор, матрица которого равна
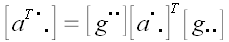 .
Сопряженный оператор называется еще транспонированным, поскольку в
ортонормированной системе
.
Сопряженный оператор называется еще транспонированным, поскольку в
ортонормированной системе
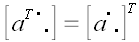 .
.
Следовательно, обратная матрица произвольного ортогонального
оператора и оператора поворота в частности равна матрице сопряженного
оператора.

В свое время мы отложили полное доказательство теоремы о том, что объем
параллелепипеда, построенного на векторах, равен определителю,
составленному из координат этих векторов. Сейчас, после проделанной
нами работы, эти лучшие времена настали.
Пусть
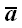 ,
,
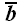 и
и
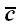 произвольные некомпланарные векторы, проведенные из начала декартовой
системы координат. Составим из координат этих векторов матрицу:
произвольные некомпланарные векторы, проведенные из начала декартовой
системы координат. Составим из координат этих векторов матрицу:
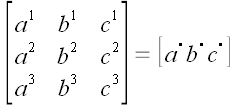 .
.
Повернем все три вектора как жесткое целое относительно оси x
таким образом, чтобы вектор
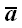 совместился бы с плоскостью xoy.
Пусть
совместился бы с плоскостью xoy.
Пусть
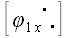 матрица оператора, который такое действие выполняет. Умножив матрицу
координат векторов на
матрица оператора, который такое действие выполняет. Умножив матрицу
координат векторов на
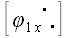 ,
мы получим новые координаты этих векторов после поворота:
,
мы получим новые координаты этих векторов после поворота:
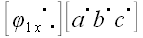 .
.
Повернем теперь все векторы относительно оси z
так, чтобы вектор
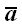 совместился бы с осью x. Угол
поворота выберем так, чтобы направления оси и вектора совпали бы
тоже. Чтобы получить новые координаты векторов, нам теперь необходимо
последнее выражение умножить на матрицу:
совместился бы с осью x. Угол
поворота выберем так, чтобы направления оси и вектора совпали бы
тоже. Чтобы получить новые координаты векторов, нам теперь необходимо
последнее выражение умножить на матрицу:
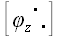 :
:
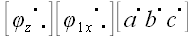 .
.
Теперь снова повернем все векторы относительно оси x
так, чтобы вектор
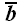 оказался в плоскости xoy с
положительной стороны оси y. Новые
координаты векторов мы получим из выражения
оказался в плоскости xoy с
положительной стороны оси y. Новые
координаты векторов мы получим из выражения
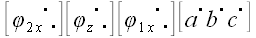 ,
где
,
где
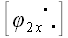 – матрица оператора, выполняющего соответствующий поворот.
– матрица оператора, выполняющего соответствующий поворот.
В результате этих преобразований вектор
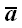 совместился с осью x, вектор
совместился с осью x, вектор
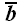 оказался в плоскости xoy с
положительной стороны оси y, а
вектор
оказался в плоскости xoy с
положительной стороны оси y, а
вектор
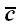 занимает некоторое положение в верхнем или нижнем полупространстве.
занимает некоторое положение в верхнем или нижнем полупространстве.
Применим теперь оператор сдвига в плоскости параллельной xoz
в направлении оси x, который
совместит вектор
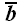 с осью y. Снова найдем новые
координаты векторов:
с осью y. Снова найдем новые
координаты векторов:
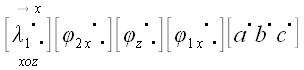 ,
где
,
где
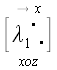 обозначает матрицу соответствующего оператора сдвига. И, наконец,
осуществим сдвиг параллельно плоскости xoy
в направлении оси y так, чтобы
вектор
обозначает матрицу соответствующего оператора сдвига. И, наконец,
осуществим сдвиг параллельно плоскости xoy
в направлении оси y так, чтобы
вектор
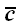 совпал с осью z. Новые координаты
векторов:
совпал с осью z. Новые координаты
векторов:
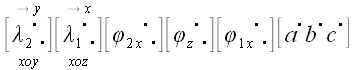 .
Мы не расписываем подробно все эти матрицы, поскольку не собираемся
их перемножать. Важно, что все эти преобразования являются
осуществимыми для произвольных некомпланарных векторов. Важно также,
что эти преобразования не изменяют ни первоначального объема
параллелепипеда, построенного на них, ни ориентации, которую они
определяют. Запишем окончательную матрицу координат векторов:
.
Мы не расписываем подробно все эти матрицы, поскольку не собираемся
их перемножать. Важно, что все эти преобразования являются
осуществимыми для произвольных некомпланарных векторов. Важно также,
что эти преобразования не изменяют ни первоначального объема
параллелепипеда, построенного на них, ни ориентации, которую они
определяют. Запишем окончательную матрицу координат векторов:
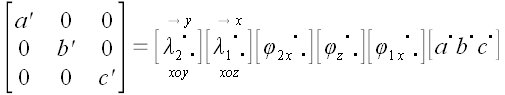 .
.
Определитель левой матрицы
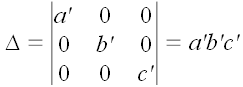 .
.
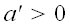 и
и
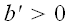 по построению. Если
по построению. Если
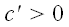 ,
то
,
то
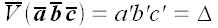 .
.
Если
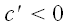 ,
то и в этом случае
,
то и в этом случае
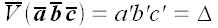 ,
поскольку векторы
,
поскольку векторы
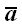 ,
,
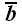 и
и
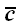 образуют левую тройку векторов.
образуют левую тройку векторов.
Но
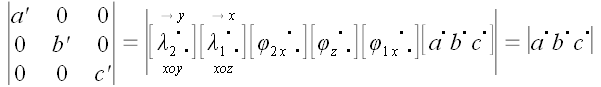 ,
,
поскольку определители всех матриц, использованных операторов, равны
единице! Следовательно, для любых трех некомпланарных векторов
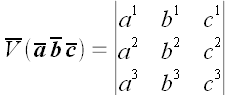 для произвольной ортонормированной системы координат. Как выражается
ориентированный объем в произвольной косоугольной системе координат,
мы уже достаточно говорили.
для произвольной ортонормированной системы координат. Как выражается
ориентированный объем в произвольной косоугольной системе координат,
мы уже достаточно говорили.
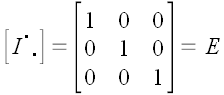 .
.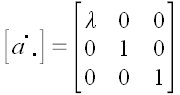 .
.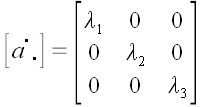 ,
где
,
где

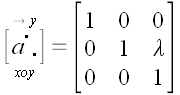 .
.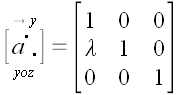 .
.
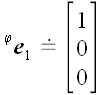 ,
,
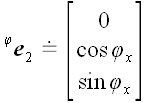 ,
,
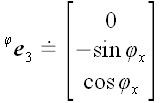 .
.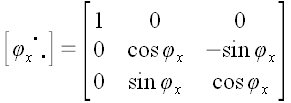
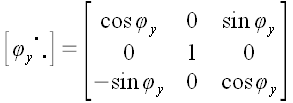 ,
,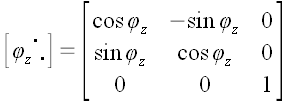 .
.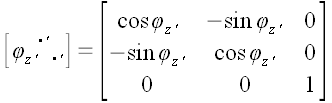 .
.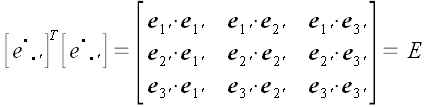 так как система координат является ортонормированной.
так как система координат является ортонормированной.
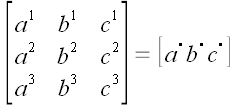 .
.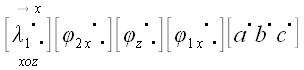 ,
где
,
где
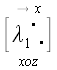 обозначает матрицу соответствующего оператора сдвига. И, наконец,
осуществим сдвиг параллельно плоскости xoy
в направлении оси y так, чтобы
вектор
обозначает матрицу соответствующего оператора сдвига. И, наконец,
осуществим сдвиг параллельно плоскости xoy
в направлении оси y так, чтобы
вектор
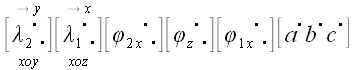 .
Мы не расписываем подробно все эти матрицы, поскольку не собираемся
их перемножать. Важно, что все эти преобразования являются
осуществимыми для произвольных некомпланарных векторов. Важно также,
что эти преобразования не изменяют ни первоначального объема
параллелепипеда, построенного на них, ни ориентации, которую они
определяют. Запишем окончательную матрицу координат векторов:
.
Мы не расписываем подробно все эти матрицы, поскольку не собираемся
их перемножать. Важно, что все эти преобразования являются
осуществимыми для произвольных некомпланарных векторов. Важно также,
что эти преобразования не изменяют ни первоначального объема
параллелепипеда, построенного на них, ни ориентации, которую они
определяют. Запишем окончательную матрицу координат векторов: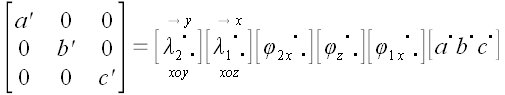 .
.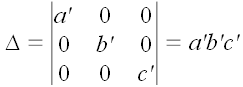 .
.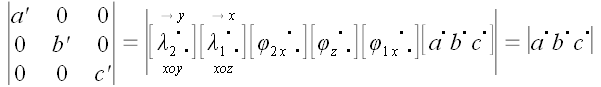 ,
,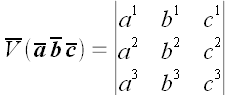 для произвольной ортонормированной системы координат. Как выражается
ориентированный объем в произвольной косоугольной системе координат,
мы уже достаточно говорили.
для произвольной ортонормированной системы координат. Как выражается
ориентированный объем в произвольной косоугольной системе координат,
мы уже достаточно говорили.